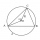
Angle ASB
On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets.
Your answer:
Your answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetryUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Central angle 2
What is the arc length of a circle with a radius of 12 cm and a central angle of 255 degrees? A. 8.5 cm B. 12π cm C. 24π cm D. 17π cm - Cut and cone
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - Circle arc angle
Points A and B lie on the circle k. The circumference of the circle k is 40 CM, and the length of the circular arc AB is 10 CM. Determine the size of the angle ABS. - Rail turn
The curve radius on a railway line is 532 m. The length of the rail track along this curve is 818 m. What is the angle ASB in degrees, where A and B are the endpoints of the curve and S is the centre of the arc? - Circle arc + section Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees.
- Circular railway
The railway connects points A, B, and C in a circular arc, whose distances are | AB | = 30 km, AC = 95 km, and BC | = 70 km. How long will the track be from A to C? - Perimeter 59
The circumference of a circular bed is 36 m. Find the length of the arc corresponding to the following central angles: 90°, 45°30′, 120°, 15°.
