Na kružnici
Na kružnici s polomerom 10 cm a so stredom S sú dané body A, B, C tak, že stredový uhol ASB má 60 stupňov a stredový uhol ASC má 90 stupňov. Určte dĺžku oblúka kružnice a veľkosť posunutí AB a AC.
Správna odpoveď:
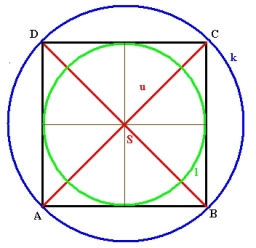
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- vektor
- aritmetika
- sčítanie
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- kruh, kružnica
- trojuholník
- kruhový oblúk
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Na kružnici 2
Na kružnici k ležia body A a B. Obvod kružnice k je 40 CM a dĺžka kružnicového oblúka AB je 10 CM. Urči veľkosť uhla ABS. - Štvorec 20
Narysujte štvorec ABCD, ktorého uhlopriečky majú dĺžku 6cm - Body ABC
Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka? - Zatáčka
Polomer zákruty na železničnej trati je 251 m. Dĺžka koľajovej dráhy na nej je 1438 m Koľko stupňov má uhol ASB, ak A, B sú okrajové body zákruty a S je stred zakrivenia (kružnicového oblúka) zákruty.
- Z7-1-6 MO 2018
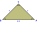Daný je rovnoramenný pravouhlý trojuholník ABS so základňou AB. Na kružnici, ktorá má stred v bode S a prechádza bodmi A a B, leží bod C tak, že trojuholník ABC je rovnoramenný. Určte, koľko bodov C vyhovuje uvedeným podmienkam, a všetky také body zostroj - Štvoruholník 13
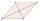Štvoruholník ABCD je súmerný podľa uhlopriečky AC. Dĺžka AC je 12 cm, dĺžka BC je 6 cm a vnútorný uhol pri vrchole B je pravý. na stranách AB, AD sú dané body E, F tak, že trojuholník ECF je rovnostranný. Určite dĺžku úsečky EF. - Narysuj 4
Narýsuj úsečku KL=55mm. Narýsuj kružnicu k so stredom K a polomerom 4cm. Vyznačuj body tak, aby patrili kružnici a spájaj ich s bodom L.
