Practice problems of the area of a circular segment
Number of problems found: 27
- The minute
 The minute hand of a clock is 6 cm long. Find the area it sweeps between 2:05 PM and 2:40 PM.
The minute hand of a clock is 6 cm long. Find the area it sweeps between 2:05 PM and 2:40 PM. - A goat 2
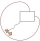 As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m². - Calculate 74794
 A wooden cylinder with a diameter of 20 cm and a length of 1 m is immersed in water. The specific weight of wood is 700kg/m³. For example, calculate the height of the wood that is above the water. The role was assigned to me as a high school freshman math
A wooden cylinder with a diameter of 20 cm and a length of 1 m is immersed in water. The specific weight of wood is 700kg/m³. For example, calculate the height of the wood that is above the water. The role was assigned to me as a high school freshman math - Horizontal 6161
 We have a horizontal tank shaped like a rainwater cylinder, 3.45 m long and 1.7 m wide. (only up to a height of 85 cm)
We have a horizontal tank shaped like a rainwater cylinder, 3.45 m long and 1.7 m wide. (only up to a height of 85 cm)
- Ratio of squares
 A circle is given in which a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares?
A circle is given in which a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares? - Corresponding 59063
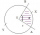 Calculate the radius and area of the circular segment if the center angle = 106° and the length of the corresponding circular arc is l = 52 cm.
Calculate the radius and area of the circular segment if the center angle = 106° and the length of the corresponding circular arc is l = 52 cm. - Trough
 How many liters of water per second can go via trough, which has a cross-section of a semicircle with a radius of 0.5 m and water speed is 142 cm per second?
How many liters of water per second can go via trough, which has a cross-section of a semicircle with a radius of 0.5 m and water speed is 142 cm per second? - Calculate 81034
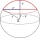 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm. - Tunnel boring
 How much material did they dig when cutting the 400m long tunnel? The area of the circular segment, which is the cross-section of the tunnel, is 62m².
How much material did they dig when cutting the 400m long tunnel? The area of the circular segment, which is the cross-section of the tunnel, is 62m².
- Three segments
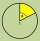 The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C?
The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C? - Circular arc
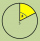 Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm²
Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm² - Semicircle
 The ornament consists of one square and four dark semicircles. The area of the square is 4 cm². Find the area of one dark semicircle and round the result to hundreds.
The ornament consists of one square and four dark semicircles. The area of the square is 4 cm². Find the area of one dark semicircle and round the result to hundreds. - Circular segment
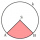 What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²?
What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²? - Circumferential 8399
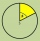 A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
- Automatic 45711
 What grass area can the automatic sprayer spray if it is set to spray at an angle of 120 ° and the water sprays up to a maximum distance of 5 meters?
What grass area can the automatic sprayer spray if it is set to spray at an angle of 120 ° and the water sprays up to a maximum distance of 5 meters? - A cell tower
 A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal?
A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal? - Arc and segment
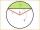 Calculate the length of circular arc l, area of the circular arc S1 and area of circular segment S2. The circle's radius is 11, and the corresponding angle is (2)/(12) π.
Calculate the length of circular arc l, area of the circular arc S1 and area of circular segment S2. The circle's radius is 11, and the corresponding angle is (2)/(12) π. - Archaeologists 81478
 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Circle segment
 A quarter circle with a radius of 4 has the same area as a circle segment with a radius of 3. What is the magnitude of the center angle of the circle segment?
A quarter circle with a radius of 4 has the same area as a circle segment with a radius of 3. What is the magnitude of the center angle of the circle segment?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
