Diagonal of Square Problems - page 12 of 18
Number of problems found: 348
- Cubes
One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm². - Axial section
The axial section of the cylinder is diagonal 45 cm long, and we know that the area of the side and the base area are in ratio 6:5. Calculate the height and radius of the cylinder base. - Support colum
Calculate the support column's volume and surface. It is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. The column height is 1. 5m. - Flowerbed
The flowerbed has the shape of a truncated pyramid. The bottom edge of the base a = 10 m, and the upper base b = 9 m. The deviation angle between the edge and the base is alpha = 45°. What volume is needed to make this flowerbed? How many plants can be pl - Horizontally 8187
We turn the prism-shaped box with a height of 1 m and a square base with an edge of 0.6 m under a force of 350 N, which acts horizontally compared to the upper edge. What is the weight of the box? - Quadrilateral prism + water
We poured water up to a height of 34 cm into a container of a regular quadrilateral prism with a base edge a = 10.6 cm and a wall diagonal of 3.9 dm. We then inserted a 6 cm long cylinder with a diameter of 10 cm. How many liters of water overflowed? - Pyramidal 44061
A pyramidal candle with a square base has a side edge of s = 12 cm and a base edge of 4 cm. How much wax will we need to make it, and how long is the wick if it is 5% bigger than its height? - Faces diagonals
Find the cuboid volume if the cuboid's diagonals are x, y, and z (wall diagonals or three faces). Solve for x=1.6, y=1.8, z=1.6 - Quadrilateral pyramid
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Pine wood
We cut a carved beam from a pine trunk 6 m long and 35 cm in diameter. The beam's cross-section is in the shape of a square, which has the greatest area. Calculate the length of the sides of a square. Calculate the volume of lumber in cubic meters. - Calculate cuboid, diagonals
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - Dimensions - crate
A wooden crate with dimensions d=3m, e=4m, and f=3m was placed in a transport container with dimensions a=10 m, b=4m, and c=3m. What is the maximum length of a straight, rigid rod of negligible diameter that can still be placed in the container in this si - Four sided prism
Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane. - 10-centimeter-high 7638
A block with a square base is inserted into a 10-centimeter-high cylinder in such a way that its base is inscribed in the base of the cylinder. The edge of the base of the block measures 4 cm. Both bodies have the same height. Calculate the difference bet - Prism - box
The prism's base is a rectangle with a side of 7.5 cm and 12.5 cm diagonal. The volume of the prism is V = 0.9 dm³. Calculate the surface of the prism. - Forces
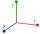In point, G acts three orthogonal forces: F1 = 16 N, F2 = 7 N, and F3 = 6 N. Determine the resultant of F and the angles between F and forces F1, F2, and F3. - Tetrahedron 83144
A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise? - Quadrilateral prism
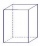Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°. - Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Rhombus base
Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 17 cm and u2 = 14 cm. The prism height is twice the base edge length.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
