Diagonal - math word problems - page 19 of 28
Number of problems found: 546
- Quadrilateral pyramid
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Side wall planes
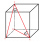Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Dimensions - crate
A wooden crate with dimensions d=3m, e=4m, and f=3m was placed in a transport container with dimensions a=10 m, b=4m, and c=3m. What is the maximum length of a straight, rigid rod of negligible diameter that can still be placed in the container in this si - Calculate cuboid, diagonals
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - The glass
The glass has the shape of a cylinder with an inner diameter of 12 cm, and the height from the bottom is 16 cm. The cut skewer can be inserted diagonally into the glass so it does not protrude beyond the edge. What is the largest possible length of the cu - Cylinder and Cuboid Volume
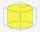A block with a square base is inserted into a 10-centimeter-high cylinder in such a way that its base is inscribed in the base of the cylinder. The edge of the base of the block measures 4 cm. Both bodies have the same height. Calculate the difference bet - Forces
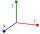In point, G acts three orthogonal forces: F1 = 16 N, F2 = 7 N, and F3 = 6 N. Determine the resultant of F and the angles between F and forces F1, F2, and F3. - Four sided prism
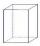Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane. - Tetrahedron water level
A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise? - Prism - box
The prism's base is a rectangle with a side of 7.5 cm and 12.5 cm diagonal. The volume of the prism is V = 0.9 dm³. Calculate the surface of the prism. - Diagonals of a prism
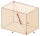The base of the square prism is a rectangle with dimensions of 3 dm and 4 dm. The height of the prism is 1 m. Find out the angle between the body diagonal and the base's diagonal. - Space diagonal angles
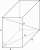Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Distance of points
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S. - Quadrilateral prism
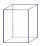Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°. - Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Trapezoidal prism
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Tetrahedral pyramid
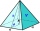Calculate the regular tetrahedral pyramid's volume and surface if the area of the base is 20 cm² and the deviation angle of the side edges from the plane of the base is 60 degrees. - Rhombus base
Calculate the volume and surface area of prisms whose base is a rhombus with diagonals u1 = 17 cm and u2 = 14 cm. The prism height is twice the base edge length. - Cuboid
Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine the angle between the body diagonal and the base plane (round to degrees). - Regular 4BH A regular quadrilateral prism has a volume of 864 cm³ and the area of its surface is twice the area of its base. Determine the size of its body diagonal.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
