Geometry construction - practice problems - page 9 of 10
Number of problems found: 181
- Intersections 2557
How many intersections do circles with radii of 10 cm and 6 cm have if the distance between their centers is 3 cm? - Perpendicular 2511
Draw a circle k/S 4.5 cm/. Next, draw: and/two mutually perpendicular diameters AB and CD b/two radii SA and SE which form an angle of 75 degrees c/chord /KL/= 4 cm d/chord /MN/, which is perpendicular to KL - Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - Hexagon - MO
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ|
- Katy MO
Kate drew a triangle ABC. The middle of the line segment AB is marked as X, and the center of the side AC is marked as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximall - Construct 1
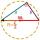Construct a triangle ABC, a = 7 cm, b = 9 cm with a right angle at C, and construct the axis of all three sides. Measure the length of side c (and write). - Straight lines
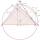Draw two lines c, d so that c || d. On line c, mark points A, and B, from point A starts perpendicular to line c, from point B perpendicular to line c. - Regular octagon
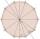Draw the regular octagon ABCDEFGH inscribed with the circle k (S; r = 2.5 cm). Select point S' so that |SS'| = 4.5 cm. Draw S (S'): ABCDEFGH - A'B'C'D'E'F'G'H'. - Square
Draw a square on the edge of a = 4 cm. Mark the center of symmetry S and all axes of symmetry. How many axes of symmetry do you have? Write down.
- Rectangle
Draw a rectangle with the sides a = 4 cm, b = 5 cm. Mark the center of symmetry S and all axes of symmetry. How many axes of symmetry? Write down. - Triangles 2157
Construct the vertices C of all triangles ABC, if given side AB, height vb on side b, and length of line tc on side c. Build all the solutions. Mark the vertices C1, C2,. .. - Square grid
A square grid consists of a square with sides of a length of 1 cm. Draw at least three patterns, each with an area of 6 cm² and a circumference of 12 cm, and their sides in a square grid. - Draw a trapezoid
Draw a trapezoid if given a = 7 cm, b = 4 cm, c = 3.5 cm, diagonal AC = 5cm. Solve as a construction task. - Triangle SSA
Construct a triangle ABC if |AB| = 5cm va = 3cm, CAB = 50 °. It is to create the analysis and construction steps.
- Right triangle
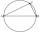Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC. - 10 pieces
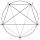How to divide the circle into ten parts (geometrically)? - Three points
Mark three points E, F, and G in the plane, not lie on one line. a) Draw a line segment FG b) Construct halfline (ray) EG c) Draw a line EF - The sum graphically
Draw a graphical sum of all sides of 4-gon ABCD. - Draw it!
Draw two lines c, d that c || d. On line c, mark points A and B. By point A, a lead perpendicular line to c. By point B, lead perpendicular line to c.
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4].Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
