Examples for secondary school students - page 176 of 231
Number of problems found: 4614
- Copper wire
 What is the weight of 1000 m copper wire with a diameter of 5 mm when metric density p = 8.8 g/cm³?
What is the weight of 1000 m copper wire with a diameter of 5 mm when metric density p = 8.8 g/cm³? - The gardener
 The gardener bought trees for 960 CZK. If every tree were cheaper by 12 CZK, he would have gotten four more trees for the same money. How many trees did he buy?
The gardener bought trees for 960 CZK. If every tree were cheaper by 12 CZK, he would have gotten four more trees for the same money. How many trees did he buy? - RT perimeter
 The leg of the rectangular triangle is 7 cm shorter than the second leg and 8 cm shorter than the hypotenuse. Calculate the triangle circumference.
The leg of the rectangular triangle is 7 cm shorter than the second leg and 8 cm shorter than the hypotenuse. Calculate the triangle circumference. - Trapezium area
 Given is a trapezoid ABCD with bases AB, CD. Let K be side AB's midpoint, and point L be side CD's midpoint. The area of triangle ALB is 15 cm2, and the area of triangle DKC is 10 cm². Calculate the area of trapezium ABCD.
Given is a trapezoid ABCD with bases AB, CD. Let K be side AB's midpoint, and point L be side CD's midpoint. The area of triangle ALB is 15 cm2, and the area of triangle DKC is 10 cm². Calculate the area of trapezium ABCD. - Row strings
 Find how many strings there are in the first row if there are 44 strings in the eighth row, and in each subsequent row, there are five more strings than in the previous row.
Find how many strings there are in the first row if there are 44 strings in the eighth row, and in each subsequent row, there are five more strings than in the previous row. - Sphere vs cube
 How much % of the surface of a sphere of radius 12 cm is the surface of a cube inscribed in this sphere?
How much % of the surface of a sphere of radius 12 cm is the surface of a cube inscribed in this sphere? - Roots count
 Substitute the numbers 0,1,2,3 into the equation as x: (x - 1) (x - 3) (x + 1) = 0 Which of them is its solution? Is there another number that solves this equation?
Substitute the numbers 0,1,2,3 into the equation as x: (x - 1) (x - 3) (x + 1) = 0 Which of them is its solution? Is there another number that solves this equation? - Inscribed sphere
 How much % of the volume of the cube whose edge is 6 meters long is the volume of a sphere inscribed in that cube?
How much % of the volume of the cube whose edge is 6 meters long is the volume of a sphere inscribed in that cube? - Siblings ages
 The average age of the siblings Standy, Radek, and Patricia are ten years. Standa is twice as old as Radek, and Patricia is two years younger than Radek. Determine the age of each sibling.
The average age of the siblings Standy, Radek, and Patricia are ten years. Standa is twice as old as Radek, and Patricia is two years younger than Radek. Determine the age of each sibling. - Wall height
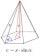 Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm.
Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm. - Four sides of trapezoid
 The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area.
The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area. - Three dice
 What is the probability that when we roll three dice, we roll the number 1,2,3?
What is the probability that when we roll three dice, we roll the number 1,2,3? - Axial cut
 The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume.
The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume. - Pyramid 4sides
 Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm.
Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm. - Support colum
 Calculate the support column's volume and surface. It is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. The column height is 1. 5m.
Calculate the support column's volume and surface. It is shaped as a vertical quadrangular prism whose base is a rhombus with diagonals u1 = 102 cm and u2 = 64 cm. The column height is 1. 5m. - Traffic cones
 Forty identical traffic cones with a base diameter d = 3 dm and height v = 6 dm will be painted orange outside (without the base). If we need 50 cm³ of paint to cover 1 m² and 1 liter of paint costs 80 SKK, how many SKK crowns will we pay?
Forty identical traffic cones with a base diameter d = 3 dm and height v = 6 dm will be painted orange outside (without the base). If we need 50 cm³ of paint to cover 1 m² and 1 liter of paint costs 80 SKK, how many SKK crowns will we pay? - Roof 8
 How many liters of air is under the tower's roof, which has the shape of a regular six-sided pyramid with a 3,6-meter-long bottom edge and a 2,5-meter height? Calculate the supporting columns occupy about 7% of the volume under the roof.
How many liters of air is under the tower's roof, which has the shape of a regular six-sided pyramid with a 3,6-meter-long bottom edge and a 2,5-meter height? Calculate the supporting columns occupy about 7% of the volume under the roof. - Apples
 A 2 kg of apples cost a certain sum of money. This sum equals the number of kilograms for which we pay 72 CZK. How much is 1 kg of apples?
A 2 kg of apples cost a certain sum of money. This sum equals the number of kilograms for which we pay 72 CZK. How much is 1 kg of apples? - Vase capacity
 The cylindrical vase is 28 cm high. Its inner diameter d = 1.1 dm. How many liters of water will fit in it if the bottom thickness is 1.5 cm?
The cylindrical vase is 28 cm high. Its inner diameter d = 1.1 dm. How many liters of water will fit in it if the bottom thickness is 1.5 cm? - Water height
 The cylindrical container with a diameter of 1.8 m contains 2000 l of water. What height does the water reach?
The cylindrical container with a diameter of 1.8 m contains 2000 l of water. What height does the water reach?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
