Examples for secondary school students - page 96 of 231
Number of problems found: 4608
- wheat 20833
 Mr. Vávra sows wheat and rye for a total of 28 ha. Rye sows two and a half times the area of wheat. How many ha sow wheat and how much rye?
Mr. Vávra sows wheat and rye for a total of 28 ha. Rye sows two and a half times the area of wheat. How many ha sow wheat and how much rye? - The angle of view
 Determine the angle of view at which the observer sees a rod 16 m long when it is 18 m from one end and 27 m from the other.
Determine the angle of view at which the observer sees a rod 16 m long when it is 18 m from one end and 27 m from the other. - Two groves
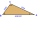 Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'?
Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'? - Individual 20463
 There are 59 pupils in the 9th grade. In 9A, there are 15% more pupils than in 9B. In 9C, there are 20% fewer than in 9B. How many pupils are in individual classes?
There are 59 pupils in the 9th grade. In 9A, there are 15% more pupils than in 9B. In 9C, there are 20% fewer than in 9B. How many pupils are in individual classes? - Contestants
 The three best contestants will divide the total prize of CZK 4,200. The second gets 20% more than the third, and the first gets 200 CZK less than the second and third together. Thus, the total prize will be CZK 4,200.
The three best contestants will divide the total prize of CZK 4,200. The second gets 20% more than the third, and the first gets 200 CZK less than the second and third together. Thus, the total prize will be CZK 4,200. - Together - parents
 Pavel received half as much money from his parents as Petr and Milan half as much as Pavel. How much did all the boys get together? The parents gave Milan CZK 1,350.
Pavel received half as much money from his parents as Petr and Milan half as much as Pavel. How much did all the boys get together? The parents gave Milan CZK 1,350. - Triangular prism - regular
 The regular triangular prism is 7 cm high. Its base is an equilateral triangle whose height is 3 cm. Calculate the surface and volume of this prism.
The regular triangular prism is 7 cm high. Its base is an equilateral triangle whose height is 3 cm. Calculate the surface and volume of this prism. - Permille of alcohol
 I have 2 per mille of alcohol in my blood. How many milliliters is it when I have 5 liters of blood?
I have 2 per mille of alcohol in my blood. How many milliliters is it when I have 5 liters of blood? - Circumference 20323
 A triangle with sides a, b, and c whose circumference is 26 cm is true: ratio a:b is 4:3, and ratio b:c is 1:2. Find the lengths of the sides of this triangle.
A triangle with sides a, b, and c whose circumference is 26 cm is true: ratio a:b is 4:3, and ratio b:c is 1:2. Find the lengths of the sides of this triangle. - Hemisphere cut
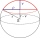 Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm.
Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm. - Five element
 The geometric sequence is given by quotient q = 1/2 and the sum of the first six members S6 = 63. Find the fifth element a5.
The geometric sequence is given by quotient q = 1/2 and the sum of the first six members S6 = 63. Find the fifth element a5. - Cube in sphere
 The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume?
The cube is inscribed in a sphere with a radius r = 6 cm. What percentage is the cube's volume from the ball's volume? - Arithmetic 20153
 The teacher has 12 examples from geometry and 15 examples from arithmetic. How many papers can he create if he wants three examples from geometry and five from arithmetic in the letter?
The teacher has 12 examples from geometry and 15 examples from arithmetic. How many papers can he create if he wants three examples from geometry and five from arithmetic in the letter? - Bent scale
 Monica weighed 52 kg. Sara 54 kg. Together they weighed 111 kg. They noticed that the needle on the scale was bent. How much did they really weigh?
Monica weighed 52 kg. Sara 54 kg. Together they weighed 111 kg. They noticed that the needle on the scale was bent. How much did they really weigh? - Horses playground
 The horse fence is a rectangular trapezoid with an area of 400 m². The base lengths should be 31 m and 19 m. If the boards are stacked in 5 rows, how many meters of fence will they need?
The horse fence is a rectangular trapezoid with an area of 400 m². The base lengths should be 31 m and 19 m. If the boards are stacked in 5 rows, how many meters of fence will they need? - Transformer 20073
 The transformer is oil-cooled and transforms a power of 20MW with an efficiency of 92%. Determine the temperature of the oil at the outlet of the transformer if the oil was 20°C when it entered the transformer. 2.5 liters of oil will flow through the tran
The transformer is oil-cooled and transforms a power of 20MW with an efficiency of 92%. Determine the temperature of the oil at the outlet of the transformer if the oil was 20°C when it entered the transformer. 2.5 liters of oil will flow through the tran - Four-member 20013
 Determine how many ways it is possible to form a four-member team from 6 men and four women, where there are exactly two men.
Determine how many ways it is possible to form a four-member team from 6 men and four women, where there are exactly two men. - Cooperative 19973
 The cooperative farmers harvested 300 tons of grain. Wheat was 25% more than oats, and rye was 96 tons less than wheat and oats combined. How many tons of wheat, rye, and oats did the cooperative harvest?
The cooperative farmers harvested 300 tons of grain. Wheat was 25% more than oats, and rye was 96 tons less than wheat and oats combined. How many tons of wheat, rye, and oats did the cooperative harvest? - Compute 4
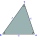 Compute the exact value of the triangle area with sides 14 mi, 12 mi, and 12 mi long.
Compute the exact value of the triangle area with sides 14 mi, 12 mi, and 12 mi long. - Compressive 19933
 The submarine is at a depth of 50 m below the concave surface of the sea. Find the hydrostatic compressive strength of seawater on a metal cover with an area of 0.6 m².
The submarine is at a depth of 50 m below the concave surface of the sea. Find the hydrostatic compressive strength of seawater on a metal cover with an area of 0.6 m².
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
