Examples for secondary school students - page 97 of 231
Number of problems found: 4608
- Cherries 19903
There are pears, apples, and cherries in the alley. There are a total of 1,075 trees. Pear is twice as much as apple, and cherry is 30% more than apple. How many trees are there? - Decide 2
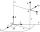Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line - Non-conforming 19863
The probability that a quality product will meet all technical requirements is 0.95. What is the probability that all three randomly produced products will be: a) conforming, b) non-conforming - Substitution 19793
Calculate in arithmetic sequence a1, d, s7, if: a1 + a4 + a6 = 71 a5 - a3 - a2 = 2 Hint: Use the substitution method when solving the system. Pay due attention to the "minus" signs in the second equation of the system. - Sum of the seventeen numbers The sum of the 17 different natural numbers is 154. Determine the sum of the two largest ones.
- Forty-eight 19513
25% of children did not attend the course because they were ill. Forty-eight children passed the course. How many children were initially supposed to complete the course? - Triangular prism
The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism. - Calculate 19443
Calculate the height of the cylinder when r = 10 mm and S = 800 mm². Calculate the radius / r / of the cylinder when the height is 20 mm and S = 1000 mm². - Quadrilateral 19413
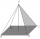Calculate the surface area of a regular quadrilateral pyramid given: a= 3.2 cm h= 19 cm Method: 1) calculation of the height of the side wall 2) area of the base 3) shell areas 4) the surface of a regular quadrilateral pyramid - Surface 19383 cone
The volume of a cone with a radius of 6 cm is 301.44 cm cubic. What is its surface? - Calculated 19363
Peter calculated the number of placement options with four teams, A, B, C, and D, in the first three places. He helped himself with a tree diagram. Complete the solution. - Intersection 19343
What is the sum of all coordinates of points at the intersection of the line p: x = -1-2t, y = 5-4t, z = -3 + 6t, where t is a real number, with the coordinate planes xy and yz? - Block or cuboid
The wall diagonals of the block have sizes of √29cm, √34cm, and √13cm. Calculate the surface and volume of the block. - Chord BC
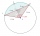A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - Vector perpendicular
Find the vector a = (2, y, z) so that a⊥ b and a ⊥ c where b = (-1, 4, 2) and c = (3, -3, -1) - Average speed
A car traveled from city A to city B at a speed of 40 km/h, then from B to C at 60 km/h, and finally from C to D at 50 km/h. Calculate the car's average speed over the entire route from A to D if the distance from A to B is 20% of the total distance and f - Table and chairs
Four people should sit at a table in front of a row of 7 chairs. What is the probability that there will be no empty chairs between them if people randomly choose their place? - Tiles
The tile is square and has a side of 15 cm. What dimensions can a rectangle composed of 90 tiles have so that no tile remains? - Trapezoid: 18703
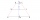In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Speedometer 18693
The Macháček family went on a 3-day trip to Třeboň. They didn't want to get too tired but wanted to see a lot. Therefore, they drove at a walking pace, and at the end of the 3rd day, they measured 90 km on the speedometer. On the second day, they traveled
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
