Length + expression of a variable from the formula - practice problems
Number of problems found: 627
- NYC block
 Bijan wants to go running during his family's vacation to New York City. To do so, he will run a neighborhood block 20 times. Bijan runs a total of 8 miles. The block has a length of 3/20 miles. Use the formula for the perimeter of the neighborhood block
Bijan wants to go running during his family's vacation to New York City. To do so, he will run a neighborhood block 20 times. Bijan runs a total of 8 miles. The block has a length of 3/20 miles. Use the formula for the perimeter of the neighborhood block - Perimeter - general
 Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side.
Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side. - A rectangle 13
 A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide?
A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide? - The triangle 6
 The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning.
The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning.
- The bedroom
 The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form.
The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form. - Carla 4
 Carla is hanging a quilt that is 0.8 meters wide on a wall that is 3.3 meters wide. Carla wants the quilt to be centered on the wall. Which of the following is the most reasonable estimate for the space on either side of the quilt when it is perfectly cen
Carla is hanging a quilt that is 0.8 meters wide on a wall that is 3.3 meters wide. Carla wants the quilt to be centered on the wall. Which of the following is the most reasonable estimate for the space on either side of the quilt when it is perfectly cen - The volume 9
 The volume of a large tank is 210 yd³. its 2 2/5 yd wide and 2 4/5 yd high. What is the length of the tank?
The volume of a large tank is 210 yd³. its 2 2/5 yd wide and 2 4/5 yd high. What is the length of the tank? - Lightning strike
 In a thunderstorm, the formula M=t/5.3 gives the approximate distance, M, in miles, from a lightning strike if it takes t second to hear the thunder after seeing the lightning. If you are 5.4 miles away from the lightning flash, how long will it take the
In a thunderstorm, the formula M=t/5.3 gives the approximate distance, M, in miles, from a lightning strike if it takes t second to hear the thunder after seeing the lightning. If you are 5.4 miles away from the lightning flash, how long will it take the - The length 18
 The length of a rectangle is three times its width. Suppose the perimeter is 96 cm. Calculate the width of the rectangle.
The length of a rectangle is three times its width. Suppose the perimeter is 96 cm. Calculate the width of the rectangle.
- A right triangle
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Rectangle - general expression
 Find the area of a rectangle whose width is x-2 units and length of x+4 units.
Find the area of a rectangle whose width is x-2 units and length of x+4 units. - A cone 3
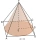 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - Polynomial rectangle
 If the length and width of a rectangle are (a² - 6a + 4) and ( -2a² - 9a + 3), find the area of the rectangle.
If the length and width of a rectangle are (a² - 6a + 4) and ( -2a² - 9a + 3), find the area of the rectangle.
- Jason 2
 Jason built a rectangular tool shed that is 888 meters wide and has an area of 969696 square meters. What is the length of Jason's tool shed?
Jason built a rectangular tool shed that is 888 meters wide and has an area of 969696 square meters. What is the length of Jason's tool shed? - Trapezoid 52
 Trapezoid perimeter = 39a-7. Three sides have the following length: 9a, 5a+1, and 17a-6. What is the length of the fourth side?
Trapezoid perimeter = 39a-7. Three sides have the following length: 9a, 5a+1, and 17a-6. What is the length of the fourth side? - A sandbox
 3/4 a sandbox has an area of 20 square feet. The length is 6 1/2 feet. What is the width of the sandbox?
3/4 a sandbox has an area of 20 square feet. The length is 6 1/2 feet. What is the width of the sandbox? - The 738
 The area of a rectangular garden is 2400 sq m. Find the width of the garden if its length is 40m.
The area of a rectangular garden is 2400 sq m. Find the width of the garden if its length is 40m. - The area 3
 The area of a rectangle is given by the expression 4x² + 5x -6. What is the length of the rectangle if its width is x+2?
The area of a rectangle is given by the expression 4x² + 5x -6. What is the length of the rectangle if its width is x+2?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
