Natural numbers - math word problems - page 66 of 92
Number of problems found: 1824
- Three-digit 69114
How many three-digit numbers have a digit sum of 6? Write the ratio of the number of created even and odd numbers and adjust it to the basic form. - Production plan
The annual production plan was exceeded by 2%. If production were higher by 300 products, the plan would be exceeded by 5%. What was the annual production plan? - Rectangle
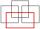The perimeter of the rectangle is 22 cm, and the area is 30 cm². Determine its dimensions if integers express the length of the sides of the rectangle in centimeters. - Unknown number 7
16% of the unknown number is 21 less than the unknown number itself. Determine the unknown natural number. - Four-digit 10261
Roman likes magic and math. Last time he conjured three- or four-digit numbers like this: • created two new numbers from the given number by dividing it between digits in the place of hundreds and tens (e.g., from the number 581, he would get 5 and 81), • - Self-counting machine
The self-counting machine works exactly like a calculator. The innkeeper wanted to add several three-digit natural numbers on his own. On the first attempt, he got the result in 2224. To check, he added these numbers again, and he got 2198. Therefore, he - Martina
Martina is solving the equation 4x - 11 = 2x + 391. Here are the first steps of her solution. 4x - 11 = 2x + 391 2x - 11 = 391 2x = 402 What did Martina do to get 2x - 11 = 391? - Number train
The numbers 1,2,3,4,5,6,7,8, and 9 traveled by train. The train had three cars, and each was carrying just three numbers. No. 1 rode in the first carriage, and in the last were all odd numbers. The conductor calculated the sum of the numbers in the first, - Divisible 68644 List all divisible numbers by six and seven that are greater than 79 and less than 91.
- Different 9711
A new bus route network was built. There are three stops on each line. In addition, every two lines either do not have a common stop or have only one common stop. What is the largest number of tracks there can be in a town if we know there are only nine d - Seven-segmet
Lenka is amused that he punched a calculator (seven-segment display) number and used only digits 2 to 9. Some numbers have the property that She again gave their image in the axial or central symmetry some number. Determine the maximum number of three-dig - Coloured numbers
Mussel wrote four different natural numbers with colored markers: red, blue, green, and yellow. When the red number is divided by blue, it gets the green number is an incomplete proportion, and yellow represents the remainder after this division. When it - Simultaneously 80392
Dulikovci, Elikovci, Filikovci, and Galikovci visited each other often last month. Each family visited each family exactly once. How many visits did all four families make together? If two families came to visit one family simultaneously, count it twice. - Winnie
Winnie Hugo had the right paw ten punches and 15 left more. How many punches do you have on the left paw? - Family trip
Dulikovci, Elikovci, Filikovci, and Galikovci visited each other often last month. Each family visited each family exactly once. How many visits did all four families make together? If two families came to visit one family simultaneously, count it twice. - Candy
How many ways can 10 identical candies be divided among 5 children? - Calculated 67234
There are 13 boys and 17 girls in the class. The weeklies are always either two girls or a boy and a girl. The teacher calculated that she has 357 ways to create a pair of weekly newspapers. However, Anetka did not come to school on Monday morning. How ma - Ninety-one 80354
Ninety-one books are arranged on seven shelves so that there are 4 more books on each subsequent shelf than on the previous one. How many books are on the 7th shelf? - Triangles
Hanka cut the 20 cm long straws into three pieces. Each piece had a length in cm. Then, with these three pieces, she tried to make a triangle. a) What circuit has each of the triangles? b) How long can the longest side measure? c) How many different trian - Rectangles - integers
How many different rectangles with integer side lengths have an area S = 60 cm²?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
