The perimeter of circular arc problems - last page
Number of problems found: 31
- Ground 8370
The arch has a radius of 3.3 m, a span of 3.25 m, and a height of 20 cm above the ground. What is the length of the arc to reach the ground? - Track arc
Two straight tracks are at an angle 74°. They will join with a circular arc with a radius r=1127 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)? - Determine 54881
On the tourist map with a scale of 1:50000, the section of the railway line between Bobrová Lhota and Javořiště is replaced by an arc of a circle with a radius of 6 cm. The arc is 90°. Determine the actual length of the track between the two villages. - Circular railway
The railway connects points A, B, and C in a circular arc, whose distances are | AB | = 30 km, AC = 95 km, and BC | = 70 km. How long will the track be from A to C?
- Disc
The circumference of the disk is 78.5 cm. What is the circumference of the circular arc of 32° on the disc? - Circumference 7143
Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci - Velocipedes
In the 19th century, bicycles had no chain drive, and the wheel axis connected the pedals directly. This wheel diameter gradually increased until the so-called high bikes (velocipedes) had a front-wheel diameter of up to 1.5 meters, while the rear wheel w - Circle arc
The circle segment has a circumference of 135.26 dm and 2096.58 dm² area. Calculate the radius of the circle and the size of the central angle. - Circular segment
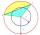Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =?
If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it.We apologize, but in this category are not a lot of examples.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
