Polygon practice problems - page 5 of 12
Number of problems found: 226
- Hexaprism container
Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm. - Rotatable tower
The rotatable tower situated in the city center has the ground shape of a regular polygon. If the tower is rotated by 18° around its centerpiece, it looks from the side same. Your task is to calculate at least how many vertices can have a ground plan view - A prism
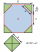A prism with an altitude of 15 cm has a base in the form of a regular octagon inscribed in a square of 10cm x 10cm. Find the volume of the prism. - Intersection 3383
A regular 15-angle is given. A triangle is formed if we connect points 3 and 7, 13 and 10. The vertices are 3 and 13, and the lines' intersections are 3.7 and 13.10. We are to determine the angle size formed by sides 3.7 and 13.10. These numbers indicate - Circle and hexagon
Calculate the radius of a circle whose circumference is 8.7 cm longer than the inscribed regular hexagon's circumference. - Center of gravity
In the isosceles triangle ABC the lengths of AB and the height to AB is the ratio of 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT. - The coordinates
The coordinates (5, 2) and (-6, 2) are vertices of a hexagon. Explain how to find the length of the segment formed by these endpoints. How long is the segment? - 6-gon
The perimeter of a regular hexagon is 154. Calculate its circumradius (radius of a circumscribed circle). - Regular octagon pad
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci - Heptagon perimeter
Calculate a regular heptagon's perimeter if its shortest diagonal length is u=14.5cm. - The rod
The rod has the shape of a regular hexagonal prism with a volume of 32.4 cubic decimetres. What is the area of the base if it is 350 centimeters long? Round to ones. - Hexagon
Divide a regular hexagon into lines with nine completely identical parts; none of them must be in a mirror image (you can only rotate individual parts arbitrarily). - Pentagon
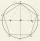Within a regular pentagon ABCDE point, P is such that the triangle is equilateral ABP. How big is the angle BCP? Make a sketch. - Hexagon in circle
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle. - Triangular 24091
A regular triangular prism with a base edge of 35 cm has a volume of 22.28 l. Calculate its height. - Inscribed 43991
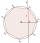An irregular convex octagon is inscribed in the circle. Its four adjacent sides have a length of 3, and the remaining four adjacent sides have a size of 2. What is the area of a given octagon? - Nonagon
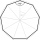Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Hexagon ABCDEF
In the regular hexagon ABCDEF, the diagonal AE has a length of 8cm. Calculate the circumference and the hexagon area. - Regular 5-gon
Calculate the area of the regular pentagon with side 16 cm. - Kites
Boys run kites on a cable of 68 meters long. What is the kite altitude if the angle from the horizontal plane is 72°?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
