Polygon practice problems - page 11 of 12
Number of problems found: 226
- A kite
ABCD is a kite. Angle OBC = 20° and angle OCD = 35°. O is the intersection of diagonals. Find angle ABC, angle ADC, and angle BAD. - ABCDEFGHIJKL 8426
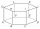The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees. - MO Z8–I–6 2018
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Hexagonal pyramid
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. - Inaccessible direct
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B, - Seats on carousel
There are 12 seats evenly distributed on the children's carousel in the shape of a circle. How long is the arm of the carousel (connecting the center of the carousel to the seat) if the distance between the two seats is 1.5m? - Hexagonal 8200
The tops of the base of a regular hexagonal pyramid lie on a circle with a radius of 10 cm. The height of the pyramid is 12cm. What is its volume? - Calculate deltoid
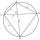Calculate the diagonals in the deltoid with sides of 10, 10, and shorter 6, 6 cm. - Interior angles
In a quadrilateral ABCD, whose vertices lie on some circle, the angle at vertex A is 58 degrees, and the angle at vertex B is 134 degrees. Calculate the sizes of the remaining interior angles. - Hexa pyramid
The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high. - Annulus
Two concentric circles with radii 1 and 9 surround the annular circle. This ring is inscribed with n circles that do not overlap. Determine the highest possible value of n. - Quadrilateral 8405
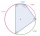Calculate the magnitude of the largest inner angle and the deviation of the diagonals in the quadrilateral, whose vertices correspond to points 1, 5, 8, and 12 on the dial. - Coordinates hexagon
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle. - Triangular prism
Calculate the surface of a regular triangular prism; the base's edges are 6 cm long, and the height of the prism is 15 cm. - Castle windows
Seven twelfth windows in the castle are in the shape of an n-gon. Six-fourteenths of these windows are quadrangular in shape, while two-ninths of them are square windows. How many windows are there in the castle if there are 15 square windows? - Hexagonal 6424
Calculate the volume and surface of a regular hexagonal prism, the base edge of which is 5 cm long and its height is 20 cm. - Perpendicular sides
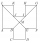In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ - Quadrilateral 82395
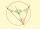The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral? - Goat
The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent - Quadrilateral pyramid
In a regular quadrilateral pyramid, the side edge is e = 7 dm, and the base's diagonal is 50 cm. Calculate the pyramid shell area.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
