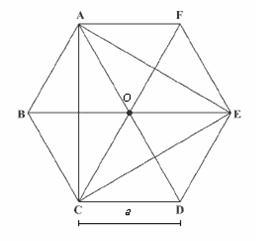
Hexagon ABCDEF
In the regular hexagon ABCDEF, the diagonal AE has a length of 8cm. Calculate the circumference and the hexagon area.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Coordinates hexagon
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle. - Determine 69304
Determine the size of the ACF angle in the regular ABCDEF hexagon. - Circle and hexagon
Calculate the radius of a circle whose circumference is 8.4 cm longer than the inscribed regular hexagon's circumference. - Circumference of edges
The hexagon pyramid has a circumference of 120 cm, and the length of the side edge is 25 cm. Calculate its volume. - Hexagon in circle
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle. - Octahedron
All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron. - Quadrilateral 47493
A regular quadrilateral prism ABCDEFGH has a base edge A B 8 cm long and 6 cm high. Point M is the center of the edge AE. Determine the distance of point M from the BDH plane.
