Maths practice for 14 year olds - page 122 of 370
Number of problems found: 7400
- Calculate 46151
 A pyramid has a square base with an edge length of 6 cm and a height of 6 cm. Calculate its surface area.
A pyramid has a square base with an edge length of 6 cm and a height of 6 cm. Calculate its surface area. - Perpendiculars 46081
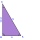 Calculate the size of the hypotenuse in a triangle if its perpendiculars are 8 cm and 8.4 cm long.
Calculate the size of the hypotenuse in a triangle if its perpendiculars are 8 cm and 8.4 cm long. - One-quarter 46001
 Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm.
Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm. - Calculate 45991
 Calculate the radius of a sphere with the same volume as a cone with a radius of 5cm and a height of 7cm.
Calculate the radius of a sphere with the same volume as a cone with a radius of 5cm and a height of 7cm. - Harvesting 45961
 The father would pick all the apples himself in 8 days. After two days, the son also started harvesting, and after another four days, they finished harvesting. How much would his son pick all the apples for?
The father would pick all the apples himself in 8 days. After two days, the son also started harvesting, and after another four days, they finished harvesting. How much would his son pick all the apples for? - Rectangular
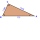 Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Surface 45911
 A large cube with an edge of length 3 is given. One small cube with a volume 27 times smaller than the volume of the large cube is glued to each of its faces. All the small cubes touch the big ones through the wall. What surface does this body have?
A large cube with an edge of length 3 is given. One small cube with a volume 27 times smaller than the volume of the large cube is glued to each of its faces. All the small cubes touch the big ones through the wall. What surface does this body have? - The quadrilateral
 The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right.
The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right. - Three-digit numbers
 How many are all three-digit numbers made up of digits 0,2,5,7 and are divisible by nine if the digits can be repeated?
How many are all three-digit numbers made up of digits 0,2,5,7 and are divisible by nine if the digits can be repeated? - Different 45881
 Silvia wants to buy a new T-shirt, skirt, and pants. The boutique has ten different T-shirts, a white and black skirt, and six types of trousers. How many different clothing options can you buy?
Silvia wants to buy a new T-shirt, skirt, and pants. The boutique has ten different T-shirts, a white and black skirt, and six types of trousers. How many different clothing options can you buy? - Performance 45861
 The electric motor with a power input of 25 kW works with an efficiency of 80 percent. He will do the work in 6 hours. What is the performance, and what part of the work is the loss?
The electric motor with a power input of 25 kW works with an efficiency of 80 percent. He will do the work in 6 hours. What is the performance, and what part of the work is the loss? - Sister 45831
 Eva has a sister who is four years older. Ten years ago, she was twice as old as Eva. How old is Eva now?
Eva has a sister who is four years older. Ten years ago, she was twice as old as Eva. How old is Eva now? - Coefficient 45821
 What is the smallest radius a turn must have for a car to enter safely without exceeding a speed of 50 km/h? The coefficient of shear friction between the tires and the surface is 0.4.
What is the smallest radius a turn must have for a car to enter safely without exceeding a speed of 50 km/h? The coefficient of shear friction between the tires and the surface is 0.4. - Percentage 45811
 There is 3.8 kg of flour in 5 kg of black bread. What percentage of the weight of bread is flour?
There is 3.8 kg of flour in 5 kg of black bread. What percentage of the weight of bread is flour? - Triangular land
 Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be?
Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be? - Factorial cancellation
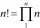 Cancel the expression with factorials: 12! x 2 x 7! / 6 x 10! 8!
Cancel the expression with factorials: 12! x 2 x 7! / 6 x 10! 8! - Equilateral triangle
 Find the area of an equilateral triangle with a side of 15 cm.
Find the area of an equilateral triangle with a side of 15 cm. - Triangle 45671
 Draw a right triangle with side a = 5 cm, c = 8 cm. The right angle is at vertex C. What is the size of side b? *
Draw a right triangle with side a = 5 cm, c = 8 cm. The right angle is at vertex C. What is the size of side b? * - Trapezoidal base
 Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, the height of trapezium v = 3.7 cm, and the height of the prism h = 5 cm.
Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, the height of trapezium v = 3.7 cm, and the height of the prism h = 5 cm. - Three pillars
 On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high?
On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
