Maths practice for 14 year olds - page 332 of 370
Number of problems found: 7397
- Pennies
 Eight hundred pennies have the same value as 100 ducats. One hundred pennies have the same value as 250 tolars. How many ducats have the same value as 100 tolars?
Eight hundred pennies have the same value as 100 ducats. One hundred pennies have the same value as 250 tolars. How many ducats have the same value as 100 tolars? - Father and son
 The father is three times older than his son. Twelve years ago, the father was nine times more senior than the son. How old are father and son?
The father is three times older than his son. Twelve years ago, the father was nine times more senior than the son. How old are father and son? - Antennas
 If you give me two antennas, it will be the same. If you give me again your two antennas, I have 5× so many more than you. How many antennas have both men?
If you give me two antennas, it will be the same. If you give me again your two antennas, I have 5× so many more than you. How many antennas have both men? - 9.A
 Class 9A has more than 20 students but fewer than 40 students. A third of the pupils wrote a math test to mark 1, the sixth to mark 2, and the ninth to mark 3. No one gets a mark of 4. How many students of class 9A wrote a test to mark 5?
Class 9A has more than 20 students but fewer than 40 students. A third of the pupils wrote a math test to mark 1, the sixth to mark 2, and the ninth to mark 3. No one gets a mark of 4. How many students of class 9A wrote a test to mark 5? - The cylindrical container
 The container has a cylindrical shape. The base diameter 0.8 meters has an area of the base equal to the shell's area. How many full liters of water can be poured maximally into the container?
The container has a cylindrical shape. The base diameter 0.8 meters has an area of the base equal to the shell's area. How many full liters of water can be poured maximally into the container? - Tin with oil
 Tin with oil has the shape of a rotating cylinder whose height is equal to the diameter of its base. The canned surface is 1884 cm². Calculate how many liters of oil are in the tin.
Tin with oil has the shape of a rotating cylinder whose height is equal to the diameter of its base. The canned surface is 1884 cm². Calculate how many liters of oil are in the tin. - Passenger car
 A passenger car covers 1 km in 2/3 minutes, and a truck in 50 seconds longer. How much slower is the speed of the truck?
A passenger car covers 1 km in 2/3 minutes, and a truck in 50 seconds longer. How much slower is the speed of the truck? - Profits
 Two members will make a profit of 52,000 EUR. The first earned 8% more and the second 10% more and thus earned 56,700 EUR together. How much will each initially earn?
Two members will make a profit of 52,000 EUR. The first earned 8% more and the second 10% more and thus earned 56,700 EUR together. How much will each initially earn? - Right triangle
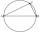 Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC.
Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC. - Clocks
 How long does the track travel the second hand of a clock in 30 hours, which is 4 cm long?
How long does the track travel the second hand of a clock in 30 hours, which is 4 cm long? - Bank deposit
 Ms. Jana, after the withdrawal amount of 2,500 euros after a year of saving in the bank. What was her deposit if the interest rate was 2.5% p.a?
Ms. Jana, after the withdrawal amount of 2,500 euros after a year of saving in the bank. What was her deposit if the interest rate was 2.5% p.a? - Stock
 Enterprise sold 7/12 of its products to foreign markets, and 2/5 of the remainder was sold at home. How many % of the products are still in stock?
Enterprise sold 7/12 of its products to foreign markets, and 2/5 of the remainder was sold at home. How many % of the products are still in stock? - Two workers
 Two workers together execute some work in 10 days. The first worker would have done it himself in 20 days. How many days would they have done himself a second worker?
Two workers together execute some work in 10 days. The first worker would have done it himself in 20 days. How many days would they have done himself a second worker? - Car rent
 Rental cars are paid a fixed daily fee plus 16 cents per kilometer traveled. Samuel wants to rent a car for a day and work out, which will cost 175 euros. When paying, he got a 20% discount on the daily fee, and the cost per kilometer was unchanged. Samue
Rental cars are paid a fixed daily fee plus 16 cents per kilometer traveled. Samuel wants to rent a car for a day and work out, which will cost 175 euros. When paying, he got a 20% discount on the daily fee, and the cost per kilometer was unchanged. Samue - Holidays
 Of the 35 students in the class, seven were on holiday in Germany and just as many in Italy. Five students visited Austria. There were 21 students in none of these countries. One student visited all three. There were two students in Italy and Austria and
Of the 35 students in the class, seven were on holiday in Germany and just as many in Italy. Five students visited Austria. There were 21 students in none of these countries. One student visited all three. There were two students in Italy and Austria and - Two months
 Mars has two months, Phobos and Deimos. Phobos orbit around Mars in 7 hours 39 minutes, and Deimos in 30 hours 14 minutes. How long will the relative positions of the three celestial bodies repeat?
Mars has two months, Phobos and Deimos. Phobos orbit around Mars in 7 hours 39 minutes, and Deimos in 30 hours 14 minutes. How long will the relative positions of the three celestial bodies repeat? - Calcium and citality
 The daily dose of calcium was obtained using 0.75 liters of milk and 60 grams of cheese. a/ In the morning, I drank half a liter of milk. How much cheese must I eat to consume a daily dose of calcium? b/ I ate 50 grams of cheese. How much milk must I drin
The daily dose of calcium was obtained using 0.75 liters of milk and 60 grams of cheese. a/ In the morning, I drank half a liter of milk. How much cheese must I eat to consume a daily dose of calcium? b/ I ate 50 grams of cheese. How much milk must I drin - Tetrahedral pyramid
 Calculate the volume and surface area of a regular tetrahedral pyramid; its height is $b cm, and the length of the edges of the base is 6 cm.
Calculate the volume and surface area of a regular tetrahedral pyramid; its height is $b cm, and the length of the edges of the base is 6 cm. - Four-digit number
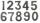 Find a four-digit number, which quadrupled written backward is the same number.
Find a four-digit number, which quadrupled written backward is the same number. - Juice box 2
 The box with juice has the shape of a cuboid. Internal dimensions are 15 cm, 20 cm, and 32 cm. Suppose the box stays at the smallest base juice level and reaches 4 cm below the upper base. How much internal volume of the box fills juice? How many cm below
The box with juice has the shape of a cuboid. Internal dimensions are 15 cm, 20 cm, and 32 cm. Suppose the box stays at the smallest base juice level and reaches 4 cm below the upper base. How much internal volume of the box fills juice? How many cm below
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
