Pythagorean theorem - math word problems - page 23 of 73
Number of problems found: 1453
- Chord 2
 Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle.
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Steps
 How many steps do you save if you go square estate for diagonal (crosswise) rather than circumvent the two sides of its perimeter with 458 steps?
How many steps do you save if you go square estate for diagonal (crosswise) rather than circumvent the two sides of its perimeter with 458 steps? - Circle inscribed
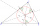 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - Square Perimeter Diagonal
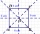 Calculate the perimeter of a square when we know the length of its diagonal e = 4.2 m
Calculate the perimeter of a square when we know the length of its diagonal e = 4.2 m - Circle's chords
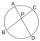 The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle.
The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle. - RR trapezoid
 Given an isosceles trapezoid ABCD with bases |AB| = 36 m, |CD| = 200 dm, and |BC| = 10m. Calculate the area and perimeter of the trapezoid and the length of the diagonal AC
Given an isosceles trapezoid ABCD with bases |AB| = 36 m, |CD| = 200 dm, and |BC| = 10m. Calculate the area and perimeter of the trapezoid and the length of the diagonal AC - In a right-angled 17
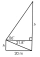 In a right-angled triangle DEF with hypotenuse f = 12 cm, the interior angle at vertex D is 60°. What is the length of the side e?
In a right-angled triangle DEF with hypotenuse f = 12 cm, the interior angle at vertex D is 60°. What is the length of the side e? - Triangle perimeter area
 What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²?
What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²? - Hypotenuse and legs
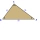 A right triangle with hypotenuse c=25 dm is given. Calculate the length of the unknown side, given: side a=15 dm. Find the area of this triangle. Sketch the triangle and describe all its vertices and sides correctly.
A right triangle with hypotenuse c=25 dm is given. Calculate the length of the unknown side, given: side a=15 dm. Find the area of this triangle. Sketch the triangle and describe all its vertices and sides correctly. - Staircase railing length
 How long is the staircase railing with 17 steps if the step is 32 cm deep and 14.5 cm high? The last step does not count.
How long is the staircase railing with 17 steps if the step is 32 cm deep and 14.5 cm high? The last step does not count. - Tree ladder height
 How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height.
How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height. - Consider 3
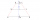 Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid.
Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid. - Michael 2
 Michael has a 35-foot ladder leaning against the side of his house. If the bottom of the ladder is 21 feet away from his house, how many feet above the ground does the ladder touch the house?
Michael has a 35-foot ladder leaning against the side of his house. If the bottom of the ladder is 21 feet away from his house, how many feet above the ground does the ladder touch the house? - Angle of diagonals
 Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°.
Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°. - Trip with compass
 During the trip, Peter went 5 km straight north from the cottage, then 12 km west, and finally returned straight to the cottage. How many kilometers did Peter cover during the whole trip?
During the trip, Peter went 5 km straight north from the cottage, then 12 km west, and finally returned straight to the cottage. How many kilometers did Peter cover during the whole trip? - Land boundary
 The land is a right triangle. Its hypotenuse is 30 meters long, and its circumference is 72 meters. What are the sizes of the remaining sides of the land boundary?
The land is a right triangle. Its hypotenuse is 30 meters long, and its circumference is 72 meters. What are the sizes of the remaining sides of the land boundary? - Right Triangle Sides Area
 In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c
In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c - Two chords
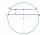 In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle.
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle. - Isosceles Right Triangle Perimeter
 In an isosceles right triangle, the arms are 50 mm long, and the height at the base is 35.35 mm. Calculate the perimeter of this triangle in millimeters.
In an isosceles right triangle, the arms are 50 mm long, and the height at the base is 35.35 mm. Calculate the perimeter of this triangle in millimeters. - Pendulum
 Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm.
Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
