Pythagorean theorem - math word problems - page 22 of 73
Number of problems found: 1449
- R Trapezium
 Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter?
Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter? - Trigonometric functions
 In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20)
In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20) - Rectangle SS
 The perimeter of a rectangle is 154 dm, and its diagonal is 62.36 dm. Find the dimensions of the rectangle.
The perimeter of a rectangle is 154 dm, and its diagonal is 62.36 dm. Find the dimensions of the rectangle. - Parallelogram 82626
 Calculate the area of a parallelogram if we know the perimeter is 23 cm, the diagonal is 8.5 cm, and one side is 1.5 cm longer.
Calculate the area of a parallelogram if we know the perimeter is 23 cm, the diagonal is 8.5 cm, and one side is 1.5 cm longer. - Calculate 8166
 Calculate the perimeter of a square when we know the length of its diagonal e = 4.2 m
Calculate the perimeter of a square when we know the length of its diagonal e = 4.2 m - Determine 6415
 Determine the distance of two parallel chords of lengths of 7 cm and 11 cm in a circle with a radius of 7 cm.
Determine the distance of two parallel chords of lengths of 7 cm and 11 cm in a circle with a radius of 7 cm. - Circle's chords
 The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle.
The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle. - Hypotenuse and legs
 A right triangle with hypotenuse c=25 dm is given. Calculate the length of the unknown side, given: side a=15 dm. Find the area of this triangle. Sketch the triangle and describe all its vertices and sides correctly.
A right triangle with hypotenuse c=25 dm is given. Calculate the length of the unknown side, given: side a=15 dm. Find the area of this triangle. Sketch the triangle and describe all its vertices and sides correctly. - Consider 3
 Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid.
Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid. - The quadrilateral
 The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right.
The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right. - Ratio of triangles areas
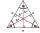 In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - Concentric circles and chord
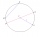 In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord?
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord? - A-shaped ladder
 An unfolded double ladder (A-shaped rung) is 10 m long. How high will it reach if the painter extends both parts of the ladder and ensures that the two parts of the ladder are 12 m apart on the ground?
An unfolded double ladder (A-shaped rung) is 10 m long. How high will it reach if the painter extends both parts of the ladder and ensures that the two parts of the ladder are 12 m apart on the ground? - Diamond diagonals
 Calculate the diamonds' diagonal lengths if the diamond area is 156 cm square and the side length is 13 cm.
Calculate the diamonds' diagonal lengths if the diamond area is 156 cm square and the side length is 13 cm. - Rectangle 3-4-5
 The sides of the rectangle are in a ratio of 3:4. The length of its diagonal is 20 cm. Calculate the area of the rectangle.
The sides of the rectangle are in a ratio of 3:4. The length of its diagonal is 20 cm. Calculate the area of the rectangle. - Dog
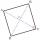 The dog is tied to a chain, which is mounted in the corner of the yard. The yard is shaped like a square with a side length of 20 meters. The same length is also a dog chain. Are there places in the yard where the dog can't reach?
The dog is tied to a chain, which is mounted in the corner of the yard. The yard is shaped like a square with a side length of 20 meters. The same length is also a dog chain. Are there places in the yard where the dog can't reach? - EQL triangle
 Calculate the inradius and circumradius of an equilateral triangle with side a=67 cm.
Calculate the inradius and circumradius of an equilateral triangle with side a=67 cm. - Rhombus and inscribed circle
 It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals.
It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals. - Circumscribed 83152
 Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle.
Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle. - Staircase 81963
 How long is the staircase railing with 17 steps if the step is 32 cm deep and 14.5 cm high? The last step does not count.
How long is the staircase railing with 17 steps if the step is 32 cm deep and 14.5 cm high? The last step does not count.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
