Right triangle practice problems - page 4 of 86
Number of problems found: 1720
- Slant height 3
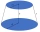 The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height.
The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height. - Triangle
 Can an equilateral triangle have a right angle?
Can an equilateral triangle have a right angle? - Perpendicular sides
 In a right triangle, one perpendicular is 1 m shorter than the hypotenuse. The other perpendicular is 2 m shorter than the hypotenuse. Find the lengths of all sides of the triangle.
In a right triangle, one perpendicular is 1 m shorter than the hypotenuse. The other perpendicular is 2 m shorter than the hypotenuse. Find the lengths of all sides of the triangle. - Laws
 From which law directly follows the validity of Pythagoras' theorem in the right triangle? ...
From which law directly follows the validity of Pythagoras' theorem in the right triangle? ... - Euclid2
 The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle.
The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle. - Angle
 Determine the size of the smallest internal angle of a right triangle which angles forming the successive members of the arithmetic sequence.
Determine the size of the smallest internal angle of a right triangle which angles forming the successive members of the arithmetic sequence. - Isosceles triangle
 Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm.
Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm. - Area of RT 2
 Calculate the area of a right triangle whose legs have a length of 9 cm and 6.4 cm.
Calculate the area of a right triangle whose legs have a length of 9 cm and 6.4 cm. - Right triangle
 Right triangle legs have lengths 71 dm and 919 mm. Calculate the area of this triangle.
Right triangle legs have lengths 71 dm and 919 mm. Calculate the area of this triangle. - One leg
 One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle.
One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle. - Height of right RT
 The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle?
The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle? - Hypotenuse 82331
 Given a right triangle KLM with a right angle at M. What is the magnitude of the hypotenuse m if the magnitude of the normal to the hypotenuse m is 4?
Given a right triangle KLM with a right angle at M. What is the magnitude of the hypotenuse m if the magnitude of the normal to the hypotenuse m is 4? - Right triangle - legs
 Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm.
Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm. - Is right triangle
 Decide if the triangle XYZ is rectangular: x = 4 m, y = 6 m, z = 4 m
Decide if the triangle XYZ is rectangular: x = 4 m, y = 6 m, z = 4 m - Complementary angles 2
 Two complementary angles are (x+4) and (2x - 7). Find the value of x.
Two complementary angles are (x+4) and (2x - 7). Find the value of x. - Supported 6172
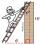 The ladder is 1.4 m from the wall and touches 3 m high. How long is the ladder?
The ladder is 1.4 m from the wall and touches 3 m high. How long is the ladder? - Broken tree
 The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree.
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree. - Iso triangle
 An isosceles triangle with a base of 8 cm. Its circumference is 28 cm. Calculate the height of the triangle.
An isosceles triangle with a base of 8 cm. Its circumference is 28 cm. Calculate the height of the triangle. - Bisector 2
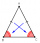 ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - The triangle
 The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle?
The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
