Angle
Determine the size of the smallest internal angle of a right triangle which angles forming the successive members of the arithmetic sequence.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
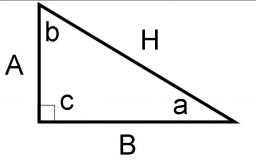
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Angle in RT
Determine the size of the smallest internal angle of a right triangle whose sides constitute the sizes of consecutive members of arithmetic progressions. - Smallest internal angle
Calculate what size has the smallest internal angle of the triangle if values of angles α:β:γ = 3:4:8 - n-gon
Gabo draws an n-gon, in which angles are consecutive members of an arithmetic sequence. The smallest angle is 70° biggest 170°. How many sides have Gabo's n-gon? - Alfa, beta, gama
In the ABC triangle, is the size of the internal angle BETA 8 degrees larger than the size of the internal angle ALFA and the size of the internal angle GAMA is twice the size of the angle BETA? Determine the size of the interior angles of the triangle AB
- Internal and external angles
Calculate a triangle's remaining internal and external angles if you know the internal angle γ (gamma) = 34 degrees and one exterior angle is 78 degrees and 40 '. Determine what kind of triangle it is from the size of its angles. - Determine 83240
In triangle ABC, the internal angle beta is twice the size of the angle alpha, and the angle gamma is 20 degrees less than the size of the angle beta. Determine the size of all interior angles of this triangle. - The chord
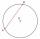A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°?
