Square (second power, quadratic) - math word problems - page 115 of 150
Number of problems found: 2994
- Diameter 3545
 A 2.4 m wide path will be paved around a circular lake with a diameter of 8.2 m. How much will the paving cost when 1m square costs 350 kc?
A 2.4 m wide path will be paved around a circular lake with a diameter of 8.2 m. How much will the paving cost when 1m square costs 350 kc? - Rectangles: 3540
 The dimensions of the left rectangle are 4 cm and (x+1) cm. The right rectangle consists of two rectangles: the upper one with dimensions of 3 cm and x cm and the lower one with an area of 7 cm². We know that the area of the left rectangle is the same as
The dimensions of the left rectangle are 4 cm and (x+1) cm. The right rectangle consists of two rectangles: the upper one with dimensions of 3 cm and x cm and the lower one with an area of 7 cm². We know that the area of the left rectangle is the same as - Everything 3536
 The cabinet for storing garden tools is shaped like a cube with an edge length of 2 m. How many m² of paint will we need to paint this cabinet if we paint everything except the bottom base? How much will it cost to paint a cabinet if one can of paint for
The cabinet for storing garden tools is shaped like a cube with an edge length of 2 m. How many m² of paint will we need to paint this cabinet if we paint everything except the bottom base? How much will it cost to paint a cabinet if one can of paint for - Parabola 3
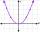 Find the equation of a parabola with its focus at (0,2) and its vertex at the origin. f: y=x²+bx+c
Find the equation of a parabola with its focus at (0,2) and its vertex at the origin. f: y=x²+bx+c - Dimensions 3531
 The room has the shape of a rectangle measuring 6m and 5m, the children's room has dimensions of 5m and 4m, and the bedroom has the shape of a square measuring 4m. How many m² of floating floors do they need in all rooms?
The room has the shape of a rectangle measuring 6m and 5m, the children's room has dimensions of 5m and 4m, and the bedroom has the shape of a square measuring 4m. How many m² of floating floors do they need in all rooms? - Calculate 3526
 Calculate the height size in the triangle ABC if the side length a = 20cm and the area of the triangle is 50 cm square.
Calculate the height size in the triangle ABC if the side length a = 20cm and the area of the triangle is 50 cm square. - Acceleration 3503
 What speed was the car moving until the driver started braking when it moved with a constant acceleration a = -1.2m/s² during braking until it stopped, traveling a distance of 135m?
What speed was the car moving until the driver started braking when it moved with a constant acceleration a = -1.2m/s² during braking until it stopped, traveling a distance of 135m? - The projection
 In axonometry, construct the projection of a perpendicular 4-sided pyramid with a square base ABCD in the plane. The base triangle gives the axonometry. We know the center of the base S, the point of the base A, and the height of the pyramid v.
In axonometry, construct the projection of a perpendicular 4-sided pyramid with a square base ABCD in the plane. The base triangle gives the axonometry. We know the center of the base S, the point of the base A, and the height of the pyramid v. - Intersection 3486
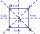 The rectangular coordinate system has a point A [-2; -4] and a point S [0; -2]. Determine the coordinates of points B, C, and D so that ABCD is a square and S is the intersection of their diagonals.
The rectangular coordinate system has a point A [-2; -4] and a point S [0; -2]. Determine the coordinates of points B, C, and D so that ABCD is a square and S is the intersection of their diagonals. - Whitewashed 3483
 The pool is in the shape of a vertical prism with a bottom in the shape of an isosceles trapezoid with dimensions of the bases of the trapezoid 10m and 18m, and arms 7m are 2m deep. During spring cleaning, the bottom and walls of the pool must be whitewas
The pool is in the shape of a vertical prism with a bottom in the shape of an isosceles trapezoid with dimensions of the bases of the trapezoid 10m and 18m, and arms 7m are 2m deep. During spring cleaning, the bottom and walls of the pool must be whitewas - Perpendicular 3482
 The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle.
The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle. - Rectangular 3478
 A segment AB is drawn in the rectangular coordinate system with endpoints A [1;6] and B [5;2]. The center symmetry is the origin of the coordinate system. Find the coordinates of the center of this segment in this symmetry projection.
A segment AB is drawn in the rectangular coordinate system with endpoints A [1;6] and B [5;2]. The center symmetry is the origin of the coordinate system. Find the coordinates of the center of this segment in this symmetry projection. - Cone
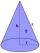 Calculate the volume of the rotating cone with a base radius of 26.3 cm and a side 38.4 cm long.
Calculate the volume of the rotating cone with a base radius of 26.3 cm and a side 38.4 cm long. - The factory
 The factory ordered 500 hexagonal steel bars in square sections with 25 mm sides. Suppose the steel density is 7,850 kg. m-3, how many cars with a load capacity of 3 tonnes will be needed to move the bars?
The factory ordered 500 hexagonal steel bars in square sections with 25 mm sides. Suppose the steel density is 7,850 kg. m-3, how many cars with a load capacity of 3 tonnes will be needed to move the bars? - Hexagonal prism
 The box of a regular hexagonal prism is 4 cm high, and the lid has sides 20 cm long. How much cardboard is needed to make it? (No part is double)
The box of a regular hexagonal prism is 4 cm high, and the lid has sides 20 cm long. How much cardboard is needed to make it? (No part is double) - Hexagonal prism 2
 The regular hexagonal prism has a surface of 140 cm² and a height of 5 cm. Calculate its volume.
The regular hexagonal prism has a surface of 140 cm² and a height of 5 cm. Calculate its volume. - Welcomed 3453
 The product of two numbers is equal to their sum. One of the numbers is four times larger than the other. Find these numbers. They welcomed that none of them were equal to zero.
The product of two numbers is equal to their sum. One of the numbers is four times larger than the other. Find these numbers. They welcomed that none of them were equal to zero. - The tent
 The tent shape of a regular quadrilateral pyramid has a base edge length of a = 2 m and a height of v = 1.8 m. If we have to add 7% of the seams, how many m² of cloth did we need to make the tent? How many m³ of air will be in the tent?
The tent shape of a regular quadrilateral pyramid has a base edge length of a = 2 m and a height of v = 1.8 m. If we have to add 7% of the seams, how many m² of cloth did we need to make the tent? How many m³ of air will be in the tent? - Cube walls
 Find the volume and surface area of the cube if the area of one wall is 40 cm².
Find the volume and surface area of the cube if the area of one wall is 40 cm². - Quadrangular prism
 The regular quadrangular prism has a base edge of 7.1 cm and a side edge of 18.2 cm long. Calculate its volume and surface area.
The regular quadrangular prism has a base edge of 7.1 cm and a side edge of 18.2 cm long. Calculate its volume and surface area.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
