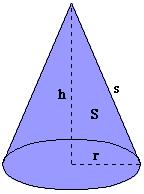
Cone
Calculate the volume of the rotating cone with a base radius of 26.3 cm and a side 38.4 cm long.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Rotating cone
Calculate the volume of a rotating cone with base radius r=18 cm and height h=20 cm. - Circumference 3370
Calculate the surface and volume of the rotating cone, whose base circumference is 125.6 cm and the side is 25 cm long. - Parameters 28521
The basic parameters of the rotating cone are: Base radius 5 cm The cone height is 12 cm, and the cone side is 13 cm. Calculate: a/volume of the cone b/cone surface - Circumference 15653
Calculate the surface and volume of a rotating cone whose base circumference is 125.6 cm and the side is 25 cm long. - Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm. - Rotating 28501
Which bags shaped like the shell of a rotating cone can hold the most popcorn? The first bag has a height of 20 cm, and the length of its side is 24 cm. The second bag has a base radius of 10 cm and a height of 25 cm. - Angle of deviation
The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane.
