Square (second power, quadratic) - math word problems - page 16 of 148
Number of problems found: 2958
- Against 82851
A 3.4 m long ladder is leaning against a wall. Its lower end is 1.6 m away from the wall. At what height does the ladder touch the wall? - Diagonals 82850
How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other? - Rectangular 82803
A rectangular flower bed, one side formed by a wall, must be fenced off with 8-meter-long mesh. What should the flower bed length be so the area is as large as possible? - Rectangle 82740
A square in a grid contains 36 squares. This is one-fifth of the number of squares of a rectangle whose side is 30 squares long. What is the length of the other side of the rectangle? Thank you - Determine 82724
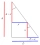A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the area of this square. - Triangulation - 3 places
Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you. - Observatories A,B
The target C is observed from two artillery observatories, A and B, 296 m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target C from observatory A. - Construction 82703
The plot of land for constructing family houses is shaped like a rectangular trapezoid with bases of 21m and 11.2m. For CZK 2,500 per square meter, the value of the land is calculated at CZK 1,352,400. What would be the length of wire mesh needed to fence - Calculate 82700
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Expression 82698
Calculate the value of the expression V = 3x²- 2x + 3 for x = -2. - Calculate 82696
In the triangle ABC, b=5 cm, c=6 cm, /BAC/ = 80° are given. Calculate the sizes of the other sides and angles, and further determine the sizes of the tangent tc and the area of the triangle. - Parallelogram 82695
Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals. - The rotation cone
The rotation cone with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume. - Calculate cone - r,h
A rotation cone with a radius of 24 cm and a height of 36 cm is given. Calculate the surface area and volume. - A raft
I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)? - Vertex of the rectangle
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circle - analytics geometry
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - The tangent of the hyperbola
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4]. - Parallelogram 82626
Calculate the area of a parallelogram if we know the perimeter is 23 cm, the diagonal is 8.5 cm, and one side is 1.5 cm longer. - Percentage 82623
The square in the picture has a side length of 6 cm. What percentage of the area is the colored part?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
