Tangent - practice problems - page 7 of 16
Number of problems found: 312
- The staircase
The staircase has a total height of 3.6 m and forms an angle of 26° with the horizontal. Calculate the length of the whole staircase. - Space diagonal angles
Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Quadrilateral pyramid
The regular quadrilateral pyramid has a base edge a = 1.56 dm and a height h = 2.05 dm. Calculate: a) the deviation angle of the sidewall plane from the base plane b) deviation angle of the side edge from the plane of the base - Calculate cone
The rotating cone has a base radius r = 226 mm, and the deviation of the side from the base plane is 56°. Calculate the height of the cone. - The tangent line
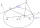Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1. - Tangents to ellipse Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1].
- Quadrilateral prism
The height of a regular quadrilateral prism is v = 10 cm, and the deviation of the body diagonal from the base is 60°. Determine the length of the base edges, the surface, and the prism's volume. - Straight road
The straight road has a rise of 19%. How big is the pitch angle? - A dodecagon
Find the surface area of a regular 12-sided polygon if its side is a = 12 cm. - Inscribed and described circle
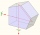Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm. - Sphere in cone
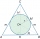A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Distance of points A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S.
- Quadrilateral pyramid
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Powerplant chimney
From the building window at the height of 7.5 m, we can see the top of the factory chimney at an altitude angle of 76° 30 ′. We can see the chimney base from the same place at a 5° 50 ′ depth angle. How tall is the chimney? - Sailboat
The 20 m long sailboat has an 8 m high mast in the middle of the deck. The top of the mast is fixed to the bow and stern with a steel cable. Determine how much cable is needed to secure the mast and what angle the cable will make with the ship's deck. - Which
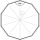Which of the following numbers is the most accurate area of a regular decagon with side s = 2 cm? (A) 9.51 cm² (B) 20 cm² (C) 30.78 cm² (D) 31.84 cm² (E) 32.90 cm2 - Pentadecagon
Calculate the area of a regular 15-side polygon inscribed in a circle with a radius r = 4. Express the result to two decimal places. - An observer
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower? - The tower
The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands? - Traffic sign
There is a traffic sign for climbing on the road with an angle of 7%. Calculate at what angle the road rises (falls).
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
