Tangent + triangle - practice problems
Number of problems found: 258
- A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - One side 4
 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
- A radio antenna
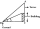 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - A right
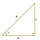 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - Horizontal 83362
 The observer sees the plane at an elevation angle of 35° (angle from the horizontal plane). At that moment, the plane reported an altitude of 4 km. How far from the observer is the place over which the aircraft flies? They circled for hundreds of meters.
The observer sees the plane at an elevation angle of 35° (angle from the horizontal plane). At that moment, the plane reported an altitude of 4 km. How far from the observer is the place over which the aircraft flies? They circled for hundreds of meters.
- Calculate 83261
 Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 - Overhangs 83158
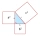 The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b.
The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b. - Horizontal 83148
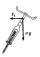 The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate.
The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate. - Determine 83083
 A 6.5-meter-long ladder rests against a vertical wall. Its lower end rests on the ground 1.6 meters from the wall. Determine how high the top of the ladder reaches and at what angle it rests against the wall.
A 6.5-meter-long ladder rests against a vertical wall. Its lower end rests on the ground 1.6 meters from the wall. Determine how high the top of the ladder reaches and at what angle it rests against the wall. - Difference 83079
 On the traffic sign that informs about the road's gradient, the figure is 6.7%. Determine the slope angle of the path. What height difference is covered by the car that traveled 2.8 km on this road?
On the traffic sign that informs about the road's gradient, the figure is 6.7%. Determine the slope angle of the path. What height difference is covered by the car that traveled 2.8 km on this road?
- Observation 82811
 From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50*10' and the bottom of the poplar at a depth angle of 58*. Calculate the height of the poplar.
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50*10' and the bottom of the poplar at a depth angle of 58*. Calculate the height of the poplar. - Observer's 82805
 An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly?
An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly? - Observation 82708
 At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation
At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation - Calculate 82696
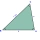 In the triangle ABC, b=5 cm, c=6 cm, /BAC/ = 80° are given. Calculate the sizes of the other sides and angles, and further determine the sizes of the tangent tc and the area of the triangle.
In the triangle ABC, b=5 cm, c=6 cm, /BAC/ = 80° are given. Calculate the sizes of the other sides and angles, and further determine the sizes of the tangent tc and the area of the triangle. - Mast angles and height
 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
See also our trigonometric triangle calculator. Tangent - practice problems. Triangle practice problems.
