Triangle practice problems - page 39 of 125
Number of problems found: 2496
- Road
The angle of a straight road is approximately 12 degrees. Determine the percentage of this road. - Triangle
Calculate the area of the right triangle ΔABC if one leg is long 12 and its opposite angle is 47°. - Descent of road
The road sign informs us the gradient is 10.9%. Calculate the angle at which the average decreases. - Bisectors
As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6. Find the perimeter of triangle △ BDE. - Angles ratio
The internal angles of a triangle are in ratio 1:4:5. What kind of triangle is it? (solve interior angles and write down and discuss) - Inequality triangle
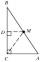The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | < c. - Isosceles triangle
What are the angles of an isosceles triangle ABC if its base is long a=7 m and has an arm b=9 m? - Bisector 2
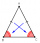ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - The triangle
The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle? - Right isosceles triangle
What can be the area of a right isosceles triangle with a side length of 8 cm? - An angle
An angle x is opposite side AB which is 10, and side AC is 15, which is the hypotenuse side in triangle ABC. Calculate angle x. - Equilateral triangle
The equilateral triangle has a 23 cm long side. Calculate its area. - Iso triangle
An isosceles triangle with a base of 8 cm. Its circumference is 28 cm. Calculate the height of the triangle. - Broken tree
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree. - Supported 6172
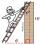The ladder is 1.4 m from the wall and touches 3 m high. How long is the ladder? - Complementary angles 2
Two complementary angles are (x+4) and (2x - 7). Find the value of x. - Right triangle - legs
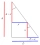Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm. - Is right triangle
Decide if the triangle XYZ is rectangular: x = 4 m, y = 6 m, z = 4 m - Hypotenuse 82331
Given a right triangle KLM with a right angle at M. What is the magnitude of the hypotenuse m if the magnitude of the normal to the hypotenuse m is 4? - One leg
One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
