Triangle practice problems - page 65 of 125
Number of problems found: 2496
- Rhombus 29
One of the diagonals of a rhombus is equal to a side of the rhombus. Find the angles of the rhombus. - Gardens
The square garden is 3/4 of the area of the triangular garden, which has sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden? - Rotating 28501
Which bags shaped like the shell of a rotating cone can hold the most popcorn? The first bag has a height of 20 cm, and the length of its side is 24 cm. The second bag has a base radius of 10 cm and a height of 25 cm. - An observer
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower? - V-belt
Calculate the length of the belt on pulleys with diameters of 105 mm and 393 mm at shaft distance 697 mm. - Circumscribed iso triangle
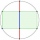Construct an isosceles triangle if a given circle circumscribed with a radius r = 2.6 cm is given. - Calculate 5789
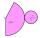Calculate the volume and surface of the rotating cone with the base radius r = 4.6dm and the height v = 230mm. - A rhombus 2
A rhombus has sides of 170 meters and a diagonal of 300 meters. What is the area of the rhombus? - Diagonal 20
The rectangular town plaza's diagonal pathway is 20 m longer than the width. Suppose the pathway is 20 m shorter than twice the width. How long should the pathway be? - Axial cut
The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume. - Right-angled triangle
The right-angled triangle XYZ is similar to the triangle ABC, which has a right angle at the vertex X. The following applies: side a = 9 cm, x=4 cm, x = v-4 (v = height of triangle ABC). Calculate the unknown side lengths of both triangles. - Distance
What is the distance between the origin and the point (-11; 13)? - Cuboid diagonal
Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees. - Airplane navigation
An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 35.95°W. How far is the plane from the airport (round to the nearest mile)? - Equilateral triangle vs circle
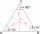Find the area of an equilateral triangle inscribed in a circle of radius r = 9 cm. What percentage of the circle area does it occupy? - Hot air balloon
The center of the balloon is at an altitude of 600 m above the ground (AGL). The observer on earth sees the center of the balloon at an elevation angle of 38°20'. The balloon is seen from the perspective of an angle of 1°16'. Calculate the diameter of the - Circumference 5254
Calculate the shorter side and the diagonal of the rectangle if one side is 2 cm longer than the other and its circumference is equal to 70 centimeters. - Rectangle 35
Find the rectangle area when the diagonal is equal to 30 cm and the width is double the length. - Billboard
A rectangular billboard is 2.5 m long with a diagonal of 2.8 m long. Calculate the perimeter and the area of the billboard. - Circle inscribed
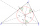There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
