Unit conversion - math word problems - page 122 of 132
Number of problems found: 2626
- De Moivre's formula
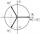 There are two distinct complex numbers, such that z³ is equal to 1 and z is not equal to 1. Calculate the sum of these two numbers.
There are two distinct complex numbers, such that z³ is equal to 1 and z is not equal to 1. Calculate the sum of these two numbers. - Theatre
 The theatrical performance started at 10:50 and ended at 13:50. How many minutes long?
The theatrical performance started at 10:50 and ended at 13:50. How many minutes long? - Liters in cylinder
 Determine the height at which level 18 liters of water in a cylindrical container having a bottom diameter 24 cm.
Determine the height at which level 18 liters of water in a cylindrical container having a bottom diameter 24 cm. - Vector sum
 The magnitude of the vector u is 2 and the magnitude of the vector v is 11. The angle between vectors is 64°. What is the magnitude of the vector u + v?
The magnitude of the vector u is 2 and the magnitude of the vector v is 11. The angle between vectors is 64°. What is the magnitude of the vector u + v? - Tetrapack
 How high should the milk box be in the shape of a prism with base dimensions 8 cm and 7.2 cm if its volume is 1 liter?
How high should the milk box be in the shape of a prism with base dimensions 8 cm and 7.2 cm if its volume is 1 liter? - Aircrafts
 Above the town, the hall tower flew the plane at a constant speed of 510 km/h, and 15 minutes later, the second plane at a speed of 703 km/h. How long and how far from the town hall will it be for aircraft to catch up?
Above the town, the hall tower flew the plane at a constant speed of 510 km/h, and 15 minutes later, the second plane at a speed of 703 km/h. How long and how far from the town hall will it be for aircraft to catch up? - Diagonals
 Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°.
Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°. - Two cars
 Car A1 goes at an average speed of 127 km/h, and the second car, A2, goes at 122 km/h. How many seconds will it take car A1 to circulate car A2? Assume that both cars are 4.7 meters long and the safety gap between cars is 2.6 meters.
Car A1 goes at an average speed of 127 km/h, and the second car, A2, goes at 122 km/h. How many seconds will it take car A1 to circulate car A2? Assume that both cars are 4.7 meters long and the safety gap between cars is 2.6 meters. - ISO trapezium
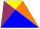 Calculate the area of an isosceles trapezoid with base 50 long, leg 12 long, and with the angle between the base and leg 70 degrees.
Calculate the area of an isosceles trapezoid with base 50 long, leg 12 long, and with the angle between the base and leg 70 degrees. - Knight
 Knight passed 36 km long track in 144 minutes. What was his average speed?
Knight passed 36 km long track in 144 minutes. What was his average speed? - Angle between vectors
 Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21)
Find the angle between the given vectors to the nearest tenth degree. u = (-1, 24) and v = (-8, -21) - 30-60-90
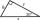 The longer leg of a 30°-60°-90° triangle measures 14. What is the length of the shorter leg?
The longer leg of a 30°-60°-90° triangle measures 14. What is the length of the shorter leg? - EQL triangle
 Calculate the inradius and circumradius of an equilateral triangle with side a=67 cm.
Calculate the inradius and circumradius of an equilateral triangle with side a=67 cm. - Flowerbed
 The flowerbed has the shape of an obtuse isosceles triangle. The arm has a size of 7.6 meters, and an angle opposite the base size is 124°. What is the distance from the base to the opposite vertex?
The flowerbed has the shape of an obtuse isosceles triangle. The arm has a size of 7.6 meters, and an angle opposite the base size is 124°. What is the distance from the base to the opposite vertex? - TV commercials
 For the typical one-hour prime-time television slot, the number of minutes of commercials is 3/8 of the actual program's minutes. Determine how many minutes of the program are shown in that one hour.
For the typical one-hour prime-time television slot, the number of minutes of commercials is 3/8 of the actual program's minutes. Determine how many minutes of the program are shown in that one hour. - Trains
 From station 130 km away started passenger train and after 2.7 hours after the express train, which travels 20 km an hour more. Express train finish journey 12 minutes early. Calculate the average speed of these two trains.
From station 130 km away started passenger train and after 2.7 hours after the express train, which travels 20 km an hour more. Express train finish journey 12 minutes early. Calculate the average speed of these two trains. - Cable car 2
 The cable car rises at an angle of 16° and connects the upper and lower station with an altitude difference of 1082 m. How long is the cable car's track?
The cable car rises at an angle of 16° and connects the upper and lower station with an altitude difference of 1082 m. How long is the cable car's track? - House roof
 The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof?
The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m² is needed to cover the roof? - Ice cream in cone
 The ice cream cone with a diameter of 5.4 cm is 1.2 dl of ice cream. Calculate the depth of the cone.
The ice cream cone with a diameter of 5.4 cm is 1.2 dl of ice cream. Calculate the depth of the cone. - Cuboid diagonal
 Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees.
Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c have dimensions in the ratio of 10:8:9. If you know that the diagonal wall AC is 75 cm, and the angle between AC and space diagonal AG is 30 degrees.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
