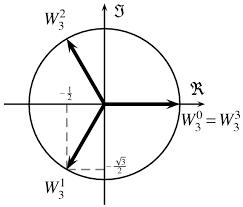
De Moivre's formula
There are two distinct complex numbers, such that z3 is equal to 1 and z is not equal to 1.
Calculate the sum of these two numbers.
Calculate the sum of these two numbers.
Correct answer:
Tips for related online calculators
Try our complex numbers calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsnumbersgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- There 33
There is a number that is three-fifths the total of the other number. When four is added to one of the numbers, their sum will be equal to the other number. There are two pairs of numbers that satisfy these descriptions. What are they? - Four-digit 67444
Emil forgot the PIN for his payment card. It knows that it is four-digit, starts with 1, ends with 2, and does not repeat digits; its digit sum is 15. How many such codes are there? List all the options. - In the shipment
There are 40 products in the shipment. Of these, 4 are defective. In how many ways can we select 5 products so that exactly 3 of them are good? - Amazing number
An amazing number is a name for such an even number, the decomposition product of prime numbers has exactly three, not necessarily different factors, and the sum of all its divisors is equal to twice that number. Find all the amazing numbers. - Is complex
Are these numbers 2i, 4i, 2i + 1, 8i, 2i + 3, 4 + 7i, 8i, 8i + 4, 5i, 6i, 3i complex? - An Argand diagram
Find the sum z1+z2 and difference z1-z2 and z2-z1 of z1=5+2i and z2=2+3i by an Argand diagram. - Four-digit number
Find all four-digit abcd numbers with a digit sum of 12 such that ab-cd = 1
