Příklady pro 8. ročník (pro osmáky) - strana 125 z 402
Počet nalezených příkladů: 8031
- Dlouhá úsečka
 Úsečka AB je dlouhá 8 cm. Rozdělte ji v poměru 2:3.
Úsečka AB je dlouhá 8 cm. Rozdělte ji v poměru 2:3. - Ve dvou 3
 Ve dvou pobočkách krejčovské dílny se mělo za rok ušít celkem 590 kusů oděvů. V první dílně se však ušilo o 30% více a ve druhé o 10%, takže bylo ušito celkem 703 kusů. Kolik výrobků měla původně ušít první pobočka?
Ve dvou pobočkách krejčovské dílny se mělo za rok ušít celkem 590 kusů oděvů. V první dílně se však ušilo o 30% více a ve druhé o 10%, takže bylo ušito celkem 703 kusů. Kolik výrobků měla původně ušít první pobočka? - Konstrukce rovnostranného trojúhelníku
 Narýsuj rovnostranný trojúhelník ABC se stranou 8,5cm. Sestroj všechny těžnice a odměř je. Jaký je rozdíl nejdelší a nejkratší z nich?
Narýsuj rovnostranný trojúhelník ABC se stranou 8,5cm. Sestroj všechny těžnice a odměř je. Jaký je rozdíl nejdelší a nejkratší z nich? - 13300kč
 13300kč rozdělit na 3 díly. 1. díl je x, 2. díl je 2/3 1.dílu, 3. díl je 2/3 2. dílu
13300kč rozdělit na 3 díly. 1. díl je x, 2. díl je 2/3 1.dílu, 3. díl je 2/3 2. dílu - Firma 3
 Firma má na začátku roku na svém účtu 5 000 000 Kč. Peníze má uloženy s 16% úrokovou mírou. Kolik činil úrok za první rok? Kolik činil úrok za druhý rok?
Firma má na začátku roku na svém účtu 5 000 000 Kč. Peníze má uloženy s 16% úrokovou mírou. Kolik činil úrok za první rok? Kolik činil úrok za druhý rok? - Kombinace oblečení
 Kolika způsoby se mohu ráno obléct, pokud si můžu vybrat z 10 triček, 8 košil a 9 kalhot? Oblékám si kalhoty plus triko nebo kalhoty plus košili.
Kolika způsoby se mohu ráno obléct, pokud si můžu vybrat z 10 triček, 8 košil a 9 kalhot? Oblékám si kalhoty plus triko nebo kalhoty plus košili. - Proud ve vodiči
 Vypočítej proud ve vodiči (v mA), jestliže je připojen ke zdroji napětí 4,5 V a jeho odpor je 20(ohm).
Vypočítej proud ve vodiči (v mA), jestliže je připojen ke zdroji napětí 4,5 V a jeho odpor je 20(ohm). - Jaké je
 Jaké je napětí v obvodu, jestliže jeho celkový odpor je 920(ohm) a proud je 250 mA?
Jaké je napětí v obvodu, jestliže jeho celkový odpor je 920(ohm) a proud je 250 mA? - Jaký je 3
 Jaký je odpor vlákna žárovky, jestliže je připojena na 9V baterii a prochází jí proud 120 mA?
Jaký je odpor vlákna žárovky, jestliže je připojena na 9V baterii a prochází jí proud 120 mA? - Močovina 3
 Močovina obsahuje 45% dusíku. Kolik tohoto hnojiva bude potřeba na 1 hektar, když náte dodat 30 kg čistého dusíku?
Močovina obsahuje 45% dusíku. Kolik tohoto hnojiva bude potřeba na 1 hektar, když náte dodat 30 kg čistého dusíku? - Horní hranice
 Strany rovnostranného trojúhelníku jsou dlouhé 9,4 cm s přesností na jedno desetinné místo. Vypočtěte horní hranici strany tohoto trojúhelníku.
Strany rovnostranného trojúhelníku jsou dlouhé 9,4 cm s přesností na jedno desetinné místo. Vypočtěte horní hranici strany tohoto trojúhelníku. - Pravděpodobnost deště
 Za loňský rok pršelo 12 dní v březnu. Jaká je pravděpodobnost, že pršelo 20. března?
Za loňský rok pršelo 12 dní v březnu. Jaká je pravděpodobnost, že pršelo 20. března? - Závorky a desetinná čísla
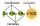 Vypočítejte příklad s desetinnými čísly: -5+(-14+11)•[24-2•(-0,4)]-{-28-41•[-8•2+4•1•(0,1-2,4)]+ 1}=
Vypočítejte příklad s desetinnými čísly: -5+(-14+11)•[24-2•(-0,4)]-{-28-41•[-8•2+4•1•(0,1-2,4)]+ 1}= - Vo výprodeji
 Kolo zlevnilo v sezónním výprodeji o 22%, což je o 88 eur. Za jakou cenu se prodává nyní?
Kolo zlevnilo v sezónním výprodeji o 22%, což je o 88 eur. Za jakou cenu se prodává nyní? - Daň státu
 15% z výnosu tržeb byla 24000kc a ta musela být odepsána jako daň státu. Jaký byl čistý zisk z tržeb?
15% z výnosu tržeb byla 24000kc a ta musela být odepsána jako daň státu. Jaký byl čistý zisk z tržeb? - Sms 2
 V lednu poslali majitelé mobilných telefonů 1 500 000 sms, což tvořilo 75% veškerých lednových sms. Kolik sms poslali zákazníci v lednu?
V lednu poslali majitelé mobilných telefonů 1 500 000 sms, což tvořilo 75% veškerých lednových sms. Kolik sms poslali zákazníci v lednu? - Film. festival
 Na film. Festivalu bylo odvysíláno 5 belgických filmů, 3 nizozemské a zbylých 33,3% filmů bylo lucemburských. Kolik filmů bylo na festivalu celkem odvysíláno?
Na film. Festivalu bylo odvysíláno 5 belgických filmů, 3 nizozemské a zbylých 33,3% filmů bylo lucemburských. Kolik filmů bylo na festivalu celkem odvysíláno? - Dvanáct
 Dvanáct malířů vymaluje všechny pokoje v hotelu za 75 hod. Kolik malířů musí provozní najmout, když musí být pokoje vymalovány za 60 hod?
Dvanáct malířů vymaluje všechny pokoje v hotelu za 75 hod. Kolik malířů musí provozní najmout, když musí být pokoje vymalovány za 60 hod? - Rozděl
 Rozděl 120 ořechů v poměru 4:6.
Rozděl 120 ořechů v poměru 4:6. - Ve třídě 16
 Ve třídě je celkem 26 žáků. Při hodnocení kontrolní práce učitel řekl: „Jedničku dostali 4 žáci, a to je 16%. “ Psali kontrolní práci všichni žáci?
Ve třídě je celkem 26 žáků. Při hodnocení kontrolní práce učitel řekl: „Jedničku dostali 4 žáci, a to je 16%. “ Psali kontrolní práci všichni žáci?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
