Příklady pro 8. ročník (pro osmáky) - strana 126 z 402
Počet nalezených příkladů: 8031
- Ve dvou obchodech
Ve dvou různých obchodech měli stejné lyže stejnou cenu. V prvním je však nejprve zdražily o 20% a pak zlevnily o 5%. Ve druhém je nejprve zlevnily o 5% a potom zdražily o 30% takže je po těchto úpravách v druhém obchodě prodávaly o 33,25 eur dražší. Jaká - Tulipány
Ze 120 tulipánů na zahradě je 45 červených, 66 žlutých, zbytek jsou žíhané. Kolik procent tulipánů na zahradě je žíhaných? - 4krát starší
Kája má 14 let. Máma 44. O kolik let bude máma 4 krát starší? - Chem. látka
Vzorek látky o hmotnosti 36 g obsahuje 91% vody. Po vysušení se hmotnost vzorku snížila na 18 g. Kolik procent vody je nyní ve vzorku? - Kolik 65
Kolik modelů aut vlastnil sběratel po sběratelské burze? Sběratel modelů aut a letadel vlastnil 3x více modelů aut než letadel. Na burze prodal 7 modelů aut a 9 modelů letadel a koupil zde 12 modelů aut a 4 modely letadel. Poté měl ve sbírce 5x více model - Na festivalu
Na festivalu tančili 4 taneční soubory. Žádný neměl méně než 10 a více než 20 členů. V každém tanci byli zastoupeni všichni tanečníci z některých dvou souborů. Nejprve bylo na pódiu 31 účastníků, pak 32, 34, 35, 37 a 38. Kolik tanečníků měly jednotlivé so - Odčítání množin
Množina B - A má dvakrát méně prvků, než množina A - B a čtyřikrát méně prvků jako množina A ∩ B. Kolikrát více prvků má množina A, jak množina B? - Dvě množiny
Pro dvě množiny K, L platí: K má 30 prvků, L má 27 prvků a množina L - K má 22 prvků. Kolik prvků má množina K - L? - Počet prvků v množinách Pro dvě neprázdné množiny A, B platí: A ∪ B má 16 prvků, A ∩ B má 11 prvků a množina A – B je prázdná. Kolik prvků má množina B-A?
- Zahrádkářská
Zahrádkářská kolonie s rozměry 180 m a 300 m má být zcela rozdělena na stejně veliké čtvercové plochy s co největším obsahem. Vypočítejte, kolik takových čtvercových ploch lze získat a určete délku strany čtverce. - Pagáče
Jano s Mišom jedli pagáče. Jano snědl o 3 více než Mišo. Součin jejich počtů (čísel) je 180. Kolik pagáčů snědl každý z nich? - Monitor 9
Urč 2/3 podílu součtu a součinu všech prvočíselných dělitelů čísla 120. - Traktor 9
Urči tlak vyvolaný pásovým traktorem o hmotnosti 30 t stojícím na vodorovné cestě, je-li obsah stykové plochy pásů se zemí 6 m čtverečních. - Hod kostkou
Vypočítejte pravděpodobnost při hodu jednou hrací kostkou, která má na stěnách čísla: 1, 2, 3, 4, 5, 6. Zapište výsledky do sešitu ve tvaru zlomku v základním tvaru takto: 2/3. a, Na kostce padne číslo 1. b, Na kostce padne číslo 5. c, Na kostce padne sud - 3 kostky
Hráč házející třemi kostkami, položil G. Galileiho otázku: "Mám vsadit na součet 11 nebo součet 12?" Co mu Galilei odpověděl? Nápověda: rozepište všechny trojice čísel, které mohou být vrženy a: mají součet 11 mají součet 12 a porovnat pravděpodobnosti. - Rozloha
Rozloha čtvercové zahrady tvoří 3/4 rozlohy trojúhelníkové zahrady se stranami 80 m, 50 m, 50 m. Kolik metrů pletiva potřebujeme na oplocení čtvercové zahrady? - Tři chlapci 2
Tři chlapci se přemístili od startu do cíle po třech různých trasách A, B, C vždy za stejný čas. Adam trasu A dlouhou 1500 m ujel na koloběžce. Bedřich trasu B dlouhou 600 m ušel pěšky. Cyril na trase C nasedl na koloběžku až po 90 m pěší chůze, koloběžku - V ostroúhlém
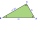V ostroúhlém trojúhelníku KLM je V průsečík jeho výšek a X je pata výšky na stranu KL. Osa úhlu XVL je rovnoběžná se stranou LM a úhel MKL má velikost 70°. Jakou velikost mají úhly KLM a KML? - Karetní hra se symboly
Peter dostal k narozeninám karetní hru. Na každé kartě jsou tři symboly. Pro karty a symboly platí tato pravidla: • každý symbol je na třech kartách, • každé dvě karty mají právě jeden společný symbol, • pro každou dvojici symbolů lze nalézt kartu, která - Cesty
Z města A do města B vedou 4 cesty. Z města B do města C vede 5 cest. Kolika různými cestami víme přijít z města A do města C přes město B?
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
