Standard deviation calculator
For standard deviation calculation, please enter numerical data separated with a comma (or space, tab, semicolon, or newline). For example: 10 20 30 40 50 60 70 80 90 100Calculation:
Statistical file:{63, 65, 68, 69, 69, 72, 75, 76, 77, 79, 79, 80, 82, 83, 84, 88, 90}
Standard deviation σ=7.6316587012832
Corrected sample standard deviation s=7.8665337310137
Other statistical characteristics:
Average (mean): μ=76.411764705882Absolute deviation: 108.58823529412
Mean deviation: 6.3875432525952
Minimum: 63
Maximum: 90
Variance: 58.242214532872
Standard deviation σ=7.6316587012832
Corrected sample standard deviation s=7.8665337310137
Coefficient of variation cV=0.10294924821188
Signal-to-noise ratio SNR=9.7135240651966
Median: 77
Quartile Q1: 69
Quartile Q2: 77
Quartile Q3: 82.5
1st decile: 64.6 (Too few data to calculate deciles)
2nd decile: 68.6
3rd decile: 70.2
4th decile: 75.2
5th decile: 77
6th decile: 79
7th decile: 81.2
8th decile: 83.4
9th decile: 88.4
Interquartile range IQR: 13.5
Quartile Deviation QD: 6.75
Coefficient of Quartile Deviation CQD: 0.089108910891089
Lower fence: 48.75
Upper fence: 102.75
Set of outliers: {} - empty set - no outliers found
Interdecile range IDR: 23.8
Mode: {69, 79} - multimodal
Geometric mean: 76.026445441703
Harmonic mean: 75.637771930754
Sum: 1299
Sum of squares: 990.11764705882
Sum of absolute values: 1299
Average absolute deviation: 6.3875432525952
Range: 27
Frequency table :
| element | frequency | cumulative frequency | relative frequency | cumulative relative frequency |
|---|---|---|---|---|
| 63 | 1 | 1 | 0.058823529411765 | 0.058823529411765 |
| 65 | 1 | 2 | 0.058823529411765 | 0.11764705882353 |
| 68 | 1 | 3 | 0.058823529411765 | 0.17647058823529 |
| 69 | 2 | 5 | 0.11764705882353 | 0.29411764705882 |
| 72 | 1 | 6 | 0.058823529411765 | 0.35294117647059 |
| 75 | 1 | 7 | 0.058823529411765 | 0.41176470588235 |
| 76 | 1 | 8 | 0.058823529411765 | 0.47058823529412 |
| 77 | 1 | 9 | 0.058823529411765 | 0.52941176470588 |
| 79 | 2 | 11 | 0.11764705882353 | 0.64705882352941 |
| 80 | 1 | 12 | 0.058823529411765 | 0.70588235294118 |
| 82 | 1 | 13 | 0.058823529411765 | 0.76470588235294 |
| 83 | 1 | 14 | 0.058823529411765 | 0.82352941176471 |
| 84 | 1 | 15 | 0.058823529411765 | 0.88235294117647 |
| 88 | 1 | 16 | 0.058823529411765 | 0.94117647058824 |
| 90 | 1 | 17 | 0.058823529411765 | 1 |
Count items: 17
Calculation of normal distribution
Sorted statistic file: {63, 65, 68, 69, 69, 72, 75, 76, 77, 79, 79, 80, 82, 83, 84, 88, 90}
How do you enter data as a frequency table?
Simple. Write data elements (separated by spaces or commas, etc.), then write f: and further write the frequency of each data item. Each element must have a defined frequency that counts numbers before and after the symbol f: must be equal. For example:1.1 2.5 3.99
f: 5 10 15
How to enter grouped data?
Grouped data are formed by aggregating individual data into groups so that a frequency distribution of these groups serves as a convenient means of summarizing or analyzing the data.| group | frequency |
| 10-20 | 5 |
| 20-30 | 10 |
| 30-40 | 15 |
10-20 20-30 30-40
f: 5 10 15
How to enter data as a cumulative frequency table?
Similar to a frequency table, but instead, f: write cf: in the second line. For example:10 20 30 40 50 60 70 80
cf: 5 13 20 32 60 80 90 100
The cumulative frequency is calculated by adding each frequency from a frequency distribution table to the sum of its predecessors. The last value will always equal the total for all observations since the calculator will have already added all frequencies to the previous total.
Practice problems from statistics:
- Z-score 3
A random variable X has a mean of 4 and a standard deviation of 2. What is the corresponding z-score for x = 7? - Squared deviation
Given the data from the problem (sample data: 23, 27, 35, 44), find the sum of the squared deviations (the numerator of the fraction under the square root in the formula). In finding the number, round all calculations to 2 decimals (if you carry more or f - Chi square
A phone battery manufacturer claims that his battery lives are approximately normally distributed with a standard deviation equal to 0.9 years. Suppose a random sample of 10 of these batteries has a standard deviation of 1.2 years. Do you think that the s - Z-score
The mean adult male pulse rate is 67.3 beats per minute, with a standard deviation of 10.3. Find the z-score for an adult male's pulse rate of 75. (Round the z-score to two decimal places. ) - A sample variance
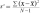Calculate the value of the sample variance. −8,−8,−3,13,4,−8,10,8 - Dispersion 3335
What is the value of the variance of the data in the file if the calculated standard deviation = 2? a) Dispersion = 6 b) Dispersion = 4 c) Dispersion = 9 d) Dispersion = 2 - Five number summary
Find the five-number summary for these data and make a boxplot. 14,5,12,19,2,35,5,4,3,7,5,8
- Dataset
Data: 11,15,11,16,12,17,13,21,14,21,15,22 Find the dispersion of a given dataset. - Dataset:
Dataset: 35 22 18 54 22 46 28 31 43 22 14 17 25 19 33 14. 1 Group the data into a grouped distribution using six classes of equal width. 2. Determine the mean, median, and mode using the raw data. 3. Draw an Ogive curve corresponding to the data and use i - IQR and range
The times spent in minutes by 20 people waiting in a queue at the bank for a teller were: 3.4, 2.1, 3.8, 2.2, 4.5, 1.4, 0,0, 1.6, 4.8, 1.5, 1.9, 0, 3.6, 5.2, 2.7, 3.0, 0.8, 3.8, 5.2, Find the range and interquartile range of the waiting times. - A student 2
A student randomly selected 225 college students and asked whether they had eaten breakfast that morning before coming to campus. Fifty-seven students were at least 25 years old, and 30 had breakfast that morning. Of the 168 students younger than 25, 82 h
more math problems »
