Výpočet směrodatné odchylky
Pro výpočet směrodatné odchylky zadejte údaje oddělené čárkou (nebo mezerou, tabulátorem, středníkem, novým řádkem apod..). Například: 10 20 30 40 50 60 70 80 90 100Jak zadat data jako frekvenční tabulku?
Jednoduše. Nejprve napište data-prvky (oddělené např. mezerou, čárkou...) pak napište f: a dále pište četnosti (frekvenci) jednotlivých dat. Každý prvek dat musí mít určenou frekvenci, tj. počet vložených čísel před a po f: se musí rovnat. Například:1.1 2.5 3.99
f: 5 10 15
Jak zadat zgrupené data?
Seskupeny údaje jsou údaje tvořeny agregací individuálních dat do skupin tak, že se rozložení četnosti těchto skupin slouží k analýze dat.| skupina | frekvence |
| 10-20 | 5 |
| 20-30 | 10 |
| 30-40 | 15 |
10-20 20-30 30-40
f: 5 10 15
Jak zadat data jako kumulatívni frekvenční tabulku?
Podobně jako jednoduchá frekvenční tabulka, ale namísto: napište cf: na druhém řádku. Například:10 20 30 40 50 60 70 80
cf: 5 13 20 32 60 80 90 100
Kumulativní frekvence se vypočítává přičtením každé frekvence z tabulky rozdělení frekvence k součtu jejích předchůdců. Poslední hodnota se vždy rovná součtu pro všechna data, protože všechny frekvence již byly přidány k předchozímu součtu
Příklady a úkoly ze statistiky:
- Test životnosti baterií
 Výrobce baterií do telefonů tvrdí, že životnost jeho baterií je přibližně normálně rozdělena se standardní odchylkou 0,9 roku. Pokud náhodný vzorek 10 těchto baterií má směrodatnou odchylku 1,2 roku. Myslíte si, že směrodatná odchylka je větší než 0,9 rok
Výrobce baterií do telefonů tvrdí, že životnost jeho baterií je přibližně normálně rozdělena se standardní odchylkou 0,9 roku. Pokud náhodný vzorek 10 těchto baterií má směrodatnou odchylku 1,2 roku. Myslíte si, že směrodatná odchylka je větší než 0,9 rok - Součet čtverců odchylek
 Vzhledem k daným údajům (vzorové údaje: 23, 27, 35, 44) najděte součet druhých mocnin odchylek (čtenář zlomku pod druhou odmocninou ve vzorci). Při hledání čísla zaokrouhlete všechny výpočty na 2 desetinná místa (pokud jich nosíte více nebo méně, možná bu
Vzhledem k daným údajům (vzorové údaje: 23, 27, 35, 44) najděte součet druhých mocnin odchylek (čtenář zlomku pod druhou odmocninou ve vzorci). Při hledání čísla zaokrouhlete všechny výpočty na 2 desetinná místa (pokud jich nosíte více nebo méně, možná bu - Rozptyl - statistika
 Dáta: 11,15,11,16,12,17,13,21,14,21,15,22 Určitě rozptyl.
Dáta: 11,15,11,16,12,17,13,21,14,21,15,22 Určitě rozptyl. - Test inflace
 Ať za posledních 14 let měla země tyto míry inflace: 6,0; 6,7; 10,4; 11,9; 7,2;3,5; 8,4; 7,5; 2,8; 4,3; 1,9; 3,9; 0,9; 0,7. Pomocí χ² testu dobré shody zjistěte, zda náhodná veličina ξ odpovídající této míře inflace má normální rozdělení nebo ne. Uvažujte
Ať za posledních 14 let měla země tyto míry inflace: 6,0; 6,7; 10,4; 11,9; 7,2;3,5; 8,4; 7,5; 2,8; 4,3; 1,9; 3,9; 0,9; 0,7. Pomocí χ² testu dobré shody zjistěte, zda náhodná veličina ξ odpovídající této míře inflace má normální rozdělení nebo ne. Uvažujte - Test normálního rozdělení
 Dotázaní respondenti odpověděli na otázku o jejich průměrné čisté měsíční mzdě. Uvedené odpovědi jsou v tis. €: 0,40; 0,60; 0,55; 0,68; 0,63; 0,70; 0,65; 0,75; 0,91; 0,63; 0,38; 0,39; 0,38; 0,74; 1,25; 1,10; 1,30; 1,15; 1,18; 1,13; 1,15; 1,19; 1,21. Pomoc
Dotázaní respondenti odpověděli na otázku o jejich průměrné čisté měsíční mzdě. Uvedené odpovědi jsou v tis. €: 0,40; 0,60; 0,55; 0,68; 0,63; 0,70; 0,65; 0,75; 0,91; 0,63; 0,38; 0,39; 0,38; 0,74; 1,25; 1,10; 1,30; 1,15; 1,18; 1,13; 1,15; 1,19; 1,21. Pomoc - Mezikvartilové rozpětí
 Časy strávené v minutách 20 lidmi čekajícími v řadě v bance na pokladníka byly: 3,4, 2,1, 3,8, 2,2, 4,5, 1,4, 0,0, 1,6, 4,8, 1,5, 1,9, 0, 3,6, 5,2, 2,7, 3,0, 0,8, 3,8, 5,2, Najděte rozsah a mezikvartilový rozsah čekacích dob.
Časy strávené v minutách 20 lidmi čekajícími v řadě v bance na pokladníka byly: 3,4, 2,1, 3,8, 2,2, 4,5, 1,4, 0,0, 1,6, 4,8, 1,5, 1,9, 0, 3,6, 5,2, 2,7, 3,0, 0,8, 3,8, 5,2, Najděte rozsah a mezikvartilový rozsah čekacích dob. - Rozptyl vzorku čísel
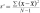 Vypočtěte hodnotu rozptylu vzorku. −8,−8,−3,13,4,−8,10,8
Vypočtěte hodnotu rozptylu vzorku. −8,−8,−3,13,4,−8,10,8 - Rozptyl ze směrodatné odchylky
 Jakou hodnotu nabývá rozptyl dat v souboru pokud vypočtená směrodatná odchylka = 2? a) Rozptyl = 6 b) Rozptyl = 4 c) Rozptyl = 9 d) Rozptyl = 2
Jakou hodnotu nabývá rozptyl dat v souboru pokud vypočtená směrodatná odchylka = 2? a) Rozptyl = 6 b) Rozptyl = 4 c) Rozptyl = 9 d) Rozptyl = 2 - Statistika podání es
 Počet es podávaných Novakem Djokovičem v posledních 20 turnajích, kterých se zúčastnil, je uveden níže. 12 17 13 7 8 14 11 14 10 12 15 9 11 13 6 15 18 5 19 24 1,1 pomocí surových dat určete rozsah (range). 1,2 Seskupte údaje do frekvenčního rozdělení s ne
Počet es podávaných Novakem Djokovičem v posledních 20 turnajích, kterých se zúčastnil, je uveden níže. 12 17 13 7 8 14 11 14 10 12 15 9 11 13 6 15 18 5 19 24 1,1 pomocí surových dat určete rozsah (range). 1,2 Seskupte údaje do frekvenčního rozdělení s ne - Seskupení dat
 Soubor údajů: 35 22 18 54 22 46 28 31 43 22 14 17 25 19 33 14. 1 Seskupte data do seskupeného rozdělení pomocí 6 tříd stejné šířky. 2. Určete průměr, medián a režim pomocí nezpracovaných údajů. 3. Nakreslete křivku O-give odpovídající údajům a použijte ji
Soubor údajů: 35 22 18 54 22 46 28 31 43 22 14 17 25 19 33 14. 1 Seskupte data do seskupeného rozdělení pomocí 6 tříd stejné šířky. 2. Určete průměr, medián a režim pomocí nezpracovaných údajů. 3. Nakreslete křivku O-give odpovídající údajům a použijte ji - 5-číselný statistický souhrn
 Najděte 5-číselný statistický souhrn těchto údajů a vytvořte si histogram (boxplot). 14,5,12,19,2,35,5,4,3,7,5,8
Najděte 5-číselný statistický souhrn těchto údajů a vytvořte si histogram (boxplot). 14,5,12,19,2,35,5,4,3,7,5,8
slovní úlohy - více »
