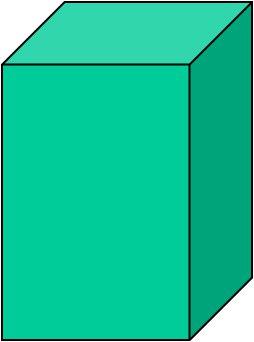
Cuboid - edges
The sum of all edges cuboid is 31 meters. However, the width is twice shorter as the length, and the height is seven times longer than the width. Determine the dimensions of the cuboid.
Final Answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Dimensions 8111
 The sum of the lengths of all block edges is 4m. The width is twice the length, and the height is seven times the width. Determine the dimensions of the block. Thank you luck
The sum of the lengths of all block edges is 4m. The width is twice the length, and the height is seven times the width. Determine the dimensions of the block. Thank you luck - Circle's chords
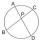 The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle.
The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle. - The length
 The length of a rectangle is 6 meters less than twice the width. If the area of the rectangle is 216 meters, find the rectangle's dimensions.
The length of a rectangle is 6 meters less than twice the width. If the area of the rectangle is 216 meters, find the rectangle's dimensions. - Diagonal 20
 The rectangular town plaza's diagonal pathway is 20 m longer than the width. Suppose the pathway is 20 m shorter than twice the width. How long should the pathway be?
The rectangular town plaza's diagonal pathway is 20 m longer than the width. Suppose the pathway is 20 m shorter than twice the width. How long should the pathway be? - Width and length
 For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle? - Water reservoir
 The cuboid reservoir contains 1900 hectoliters of water, and the water height is 2.7 m. Determine the bottom dimensions where one dimension is 2.2 m longer than the second.
The cuboid reservoir contains 1900 hectoliters of water, and the water height is 2.7 m. Determine the bottom dimensions where one dimension is 2.2 m longer than the second. - Rectangle 7768
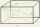 The base of a cuboid is a rectangle. The ratio of its length to width is 3:2. The length of the rectangle of the base is in the ratio of 4:5 to the height of the block. The sum of the lengths of all the edges of the block is 2.8m. Find: a) the surface of
The base of a cuboid is a rectangle. The ratio of its length to width is 3:2. The length of the rectangle of the base is in the ratio of 4:5 to the height of the block. The sum of the lengths of all the edges of the block is 2.8m. Find: a) the surface of
