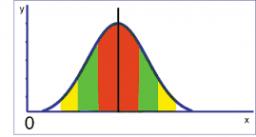
SD - mean
The mean is 10, and the standard deviation is 3.5. If the data set contains 40 data values, approximately how many of the data values will fall within the range of 6.5 to 13.5?
Correct answer:
Showing 3 comments:
Ivo
Rule 1 sigma for a normal distribution (from the average on both sides distance standard deviation sigma) lies 68.26% of the values, if are normally distributed.
Dr Math
please use our normal distribution calculator:
https://www.hackmath.net/en/calculator/normal-distribution?mean=10&sd=3.5&above=&below=&area=between&ll=6.5&ul=13.5&outsideLL=&outsideUL=&draw=Calculate
https://www.hackmath.net/en/calculator/normal-distribution?mean=10&sd=3.5&above=&below=&area=between&ll=6.5&ul=13.5&outsideLL=&outsideUL=&draw=Calculate
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
Looking for a standard deviation calculator?
Looking for a statistical calculator?
Looking for a standard deviation calculator?
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Life expectancy
 The life expectancy of batteries has a normal distribution with a mean of 350 minutes and a standard deviation of 10 minutes. What is the range in minutes 68% of the batteries will last? What is the range in minutes? How long will approximately 99.7% of b
The life expectancy of batteries has a normal distribution with a mean of 350 minutes and a standard deviation of 10 minutes. What is the range in minutes 68% of the batteries will last? What is the range in minutes? How long will approximately 99.7% of b - Bivariate data set
 Here is a bivariate data set in which you believe y to be the response variable. x y 51.4 44.8 60.2 46.6 60.1 46.8 45.8 46.3 37.4 41.8 72.4 52.5 60 48.2 67.5 49.5 60.9 49.8 51.1 45.7 62.7 49.6 194.9 84.2 Make a scatter plot of this data. Which point is an
Here is a bivariate data set in which you believe y to be the response variable. x y 51.4 44.8 60.2 46.6 60.1 46.8 45.8 46.3 37.4 41.8 72.4 52.5 60 48.2 67.5 49.5 60.9 49.8 51.1 45.7 62.7 49.6 194.9 84.2 Make a scatter plot of this data. Which point is an - Coefficient of skewness
 For the data set whose Karl Pearson's Coefficient of skewness = -2.25, variance is 16, and Mean is 35, then its median value will be:
For the data set whose Karl Pearson's Coefficient of skewness = -2.25, variance is 16, and Mean is 35, then its median value will be: - The number 5
 The number of hours per week the television is turned on is determined for each family in a sample. The mean of the data is 35 hours, and the median is 31.2 hours. Twenty-four families in the sample turned on the television for 20 hours or less for the we
The number of hours per week the television is turned on is determined for each family in a sample. The mean of the data is 35 hours, and the median is 31.2 hours. Twenty-four families in the sample turned on the television for 20 hours or less for the we
- Summaries
 A specialist teacher observes the time taken by each of the students with learning disabilities to complete a psychological task. She summaries the times using the following: Time Taken(mins) ; 1-5; 6-10; 11-12; 16-20 No. of Student ; 2 ; 4 ; 12; 4 Using
A specialist teacher observes the time taken by each of the students with learning disabilities to complete a psychological task. She summaries the times using the following: Time Taken(mins) ; 1-5; 6-10; 11-12; 16-20 No. of Student ; 2 ; 4 ; 12; 4 Using - Tennis aces
 The number of aces served by Novak Djokovic in the last 20 tournaments that he has participated in is shown below. 12 17 13 7 8 14 11 14 10 12 15 9 11 13 6 15 18 5 19 24 1.1 using the raw, determine the range. 1.2 Group the data into a frequency distribut
The number of aces served by Novak Djokovic in the last 20 tournaments that he has participated in is shown below. 12 17 13 7 8 14 11 14 10 12 15 9 11 13 6 15 18 5 19 24 1.1 using the raw, determine the range. 1.2 Group the data into a frequency distribut - Suppose 6
 Suppose the life span of a revolutionary light bulb is normally distributed with a mean life span of 70 thousand hours and a standard deviation of 3 thousand hours. If a light bulb is chosen at random: a) what is the probability the life span will be with
Suppose the life span of a revolutionary light bulb is normally distributed with a mean life span of 70 thousand hours and a standard deviation of 3 thousand hours. If a light bulb is chosen at random: a) what is the probability the life span will be with - IQR and range
 The times spent in minutes by 20 people waiting in a queue at the bank for a teller were: 3.4, 2.1, 3.8, 2.2, 4.5, 1.4, 0,0, 1.6, 4.8, 1.5, 1.9, 0, 3.6, 5.2, 2.7, 3.0, 0.8, 3.8, 5.2, Find the range and interquartile range of the waiting times.
The times spent in minutes by 20 people waiting in a queue at the bank for a teller were: 3.4, 2.1, 3.8, 2.2, 4.5, 1.4, 0,0, 1.6, 4.8, 1.5, 1.9, 0, 3.6, 5.2, 2.7, 3.0, 0.8, 3.8, 5.2, Find the range and interquartile range of the waiting times. - Complaints
 The table is given: days; complaints 0-4; 2 5-9; 4 10-14; 8 15-19; 6 20-24; 4 25-29; 3 30-34; 3 1.1 What percentage of complaints were resolved within two weeks? 1.2 calculate the mean number of days to resolve these complaints. 1.3 calculate the modal nu
The table is given: days; complaints 0-4; 2 5-9; 4 10-14; 8 15-19; 6 20-24; 4 25-29; 3 30-34; 3 1.1 What percentage of complaints were resolved within two weeks? 1.2 calculate the mean number of days to resolve these complaints. 1.3 calculate the modal nu
- Five number summary
 Find the five-number summary for these data and make a boxplot. 14,5,12,19,2,35,5,4,3,7,5,8
Find the five-number summary for these data and make a boxplot. 14,5,12,19,2,35,5,4,3,7,5,8 - Dataset:
 Dataset: 35 22 18 54 22 46 28 31 43 22 14 17 25 19 33 14. 1 Group the data into a grouped distribution using six classes of equal width. 2. Determine the mean, median, and mode using the raw data. 3. Draw an Ogive curve corresponding to the data and use i
Dataset: 35 22 18 54 22 46 28 31 43 22 14 17 25 19 33 14. 1 Group the data into a grouped distribution using six classes of equal width. 2. Determine the mean, median, and mode using the raw data. 3. Draw an Ogive curve corresponding to the data and use i - Statistical XY file
 Year; money spent on advertising; profit (three values each row) 2008 2 12 2009 5 20 2010 7 25 2011 11 26 2012 15 40 1. draw a scatter diagram depicting the data. 2. calculate the Pearson's correlation coefficient. 3. determine the linear regression equat
Year; money spent on advertising; profit (three values each row) 2008 2 12 2009 5 20 2010 7 25 2011 11 26 2012 15 40 1. draw a scatter diagram depicting the data. 2. calculate the Pearson's correlation coefficient. 3. determine the linear regression equat - A data
 A data set has the sample mean =14 and the sum of the data values=294. How many values are there in the data set?
A data set has the sample mean =14 and the sum of the data values=294. How many values are there in the data set? - Distribution 67074
 The time required to complete the test has a normal distribution with a mean of 50 minutes and a standard deviation of 10 minutes. What percentage of students take the test within 30 minutes?
The time required to complete the test has a normal distribution with a mean of 50 minutes and a standard deviation of 10 minutes. What percentage of students take the test within 30 minutes?
- Dataset
 Data: 11,15,11,16,12,17,13,21,14,21,15,22 Find dispersion of a given dataset.
Data: 11,15,11,16,12,17,13,21,14,21,15,22 Find dispersion of a given dataset. - Dispersion 3335
 What is the value of the variance of the data in the file if the calculated standard deviation = 2? a) Dispersion = 6 b) Dispersion = 4 c) Dispersion = 9 d) Dispersion = 2
What is the value of the variance of the data in the file if the calculated standard deviation = 2? a) Dispersion = 6 b) Dispersion = 4 c) Dispersion = 9 d) Dispersion = 2 - Standard deviation
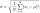 Find the standard deviation for the dataset (grouped data): Age (years); No. Of Persons 0-10 ; 15 10-20 ; 15 20-30 ; 23 30-40 ; 22 40-50 ; 25 50-60 ; 10 60-70 ; 5 70-80 ; 10
Find the standard deviation for the dataset (grouped data): Age (years); No. Of Persons 0-10 ; 15 10-20 ; 15 20-30 ; 23 30-40 ; 22 40-50 ; 25 50-60 ; 10 60-70 ; 5 70-80 ; 10
