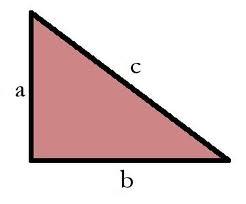
Right triangle Alef
The obvod of a right triangle is 84 cm, and the hypotenuse is 37 cm long. Determine the lengths of the legs.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- inequalities
- equation
- system of equations
- planimetrics
- right triangle
- area of a shape
- perimeter
- triangle
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circle inscribed square
 What is the area of the circle that can be inscribed in a square of 10 cm?
What is the area of the circle that can be inscribed in a square of 10 cm? - Double sides
 If each side of a triangle is doubled, then find the ratio of the area of the new triangle thus formed to the given triangle.
If each side of a triangle is doubled, then find the ratio of the area of the new triangle thus formed to the given triangle. - A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - Perimeter 83259
 The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area.
The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area.
- ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Harold
 Harold made a rectangular dog run in his backyard. The area of the dog run is 96 square feet. What are three different possible dimensions of dog run?
Harold made a rectangular dog run in his backyard. The area of the dog run is 96 square feet. What are three different possible dimensions of dog run? - Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - A raft
 I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)?
I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)? - Cone-shaped 82466
 The cone-shaped glass has a volume of 2.5 dl and a diameter of 13 cm. How much cocktail is left in the glass if the level only reaches half the height of the glass?
The cone-shaped glass has a volume of 2.5 dl and a diameter of 13 cm. How much cocktail is left in the glass if the level only reaches half the height of the glass?
- A frustum
 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Width and length
 For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle? - A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - The radius 2
 The radius of a circle is increased by 5%. What is the percentage increase in their circumference area?
The radius of a circle is increased by 5%. What is the percentage increase in their circumference area? - Two similar 2
 Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second?
Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second?
- Joey had
 Joey had 70% of his money in a savings account. The rest of his money was in a cheque account. (a). What percentage of his money was in his cheque account? (b). He had $240 in his cheque account. How much money did he have in his savings account?
Joey had 70% of his money in a savings account. The rest of his money was in a cheque account. (a). What percentage of his money was in his cheque account? (b). He had $240 in his cheque account. How much money did he have in his savings account? - A goat 2
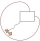 As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m². - Create 6
 Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio
Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio
