Ace
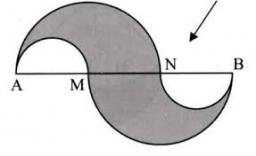
The length of segment AB is 24 cm, and the points M and N are divided into thirds. Calculate the circumference and area of this shape.
Final Answer:
Tips for related online calculators
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- MO - triangles
 On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Trapezoid 83
 Trapezoid ABCD is composed of five triangles. Points E, and G divide segment AB in the ratio 2:4:3 (in this order) into three segments. Point F is the midpoint of segment AD. Triangle AEF is isosceles and right-angled. Triangles GBC and CDG are right-angl
Trapezoid ABCD is composed of five triangles. Points E, and G divide segment AB in the ratio 2:4:3 (in this order) into three segments. Point F is the midpoint of segment AD. Triangle AEF is isosceles and right-angled. Triangles GBC and CDG are right-angl - Trapezoid thirds
 The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Rectangular trapezoid
 The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid.
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid. - Rectangular trapezoid
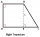 The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - Circumferential 8399
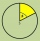 A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment. - Circumference 26361
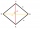 The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond.
The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond.
