Iron density
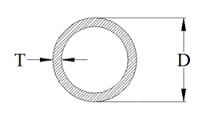
Calculate the weight of a 2 m long rail pipe with an internal diameter of 10 cm and a wall thickness of 3 mm. The iron density is p = 7.8 g/cm3.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
Tip: Our Density units converter will help you convert density units.
Do you want to convert mass units?
Do you know the volume and unit volume, and want to convert volume units?
Tip: Our Density units converter will help you convert density units.
Do you want to convert mass units?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Circle inscribed square
 What is the area of the circle that can be inscribed in a square of 10 cm?
What is the area of the circle that can be inscribed in a square of 10 cm? - Error multiplication
 In measuring the sides of a rectangle errors of 5% and 3% in excess are made. Find the error percent in the calculated area .
In measuring the sides of a rectangle errors of 5% and 3% in excess are made. Find the error percent in the calculated area . - Use the formula for area
 A parallelogram has sides of 15 cm and 12 cm. If the distance between 15 cm sides is 6 cm, find the distance between 12 cm sides.
A parallelogram has sides of 15 cm and 12 cm. If the distance between 15 cm sides is 6 cm, find the distance between 12 cm sides. - Square yards
 What is 4 1/3 yards times 5 2/3 yards?
What is 4 1/3 yards times 5 2/3 yards?
- Double sides
 If each side of a triangle is doubled, then find the ratio of the area of the new triangle thus formed to the given triangle.
If each side of a triangle is doubled, then find the ratio of the area of the new triangle thus formed to the given triangle. - Calculate 83366
 Calculate the side a of triangle ABC if we know va=8cm, b=16cm, vb=10cm.
Calculate the side a of triangle ABC if we know va=8cm, b=16cm, vb=10cm. - A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - The rectangle 7
 The rectangle shown has a length (l) of 8 and a width (w) of 6.2. A second rectangle has a length of l + 2.5 and a width of w - 1.4. Find the area of the SECOND rectangle.
The rectangle shown has a length (l) of 8 and a width (w) of 6.2. A second rectangle has a length of l + 2.5 and a width of w - 1.4. Find the area of the SECOND rectangle. - A room
 A room is 8 2/3 m by 5 1/4 m. What is the area of the room?
A room is 8 2/3 m by 5 1/4 m. What is the area of the room?
- Perimeter 83259
 The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area.
The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area. - Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be? - Ice cream company
 An ice cream company is going to open new stores in Los Angeles, New York, and Orlando. The monthly cost for a square foot of rental space in each city is as follows. town; cost/ft² Los Angeles ; $5.25 New York ; $7.25 Orlando ; $4.25 The store in Los Ang
An ice cream company is going to open new stores in Los Angeles, New York, and Orlando. The monthly cost for a square foot of rental space in each city is as follows. town; cost/ft² Los Angeles ; $5.25 New York ; $7.25 Orlando ; $4.25 The store in Los Ang - Dimensions 83176
 If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions
If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions - The capacitor
 The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate?
The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate?
- A model
 A model of a house is built on a base that measures 7 3/4 inches wide and 9 1/5 inches long. What is the area of the model house based?
A model of a house is built on a base that measures 7 3/4 inches wide and 9 1/5 inches long. What is the area of the model house based? - A rectangle 13
 A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide?
A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide? - Trim the bushes
 Mason is always helping him to trim the bushes. The area A had a length of 14 m and a breadth of 7 m, and if we are going to combine A and B, the equal is 215 m². The question is: what is the area of B?
Mason is always helping him to trim the bushes. The area A had a length of 14 m and a breadth of 7 m, and if we are going to combine A and B, the equal is 215 m². The question is: what is the area of B?
