Fraction
Fraction 0,380,38 write as fraction a/b, a, b is integers numerator/denominator.
Final Answer:

Showing 2 comments:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticnumbersGrade of the word problem
Related math problems and questions:
- Denominator 2
 The denominator of a fraction is five, and the numerator is 7. Write the fraction.
The denominator of a fraction is five, and the numerator is 7. Write the fraction. - Denominator 2883
 Write a fraction with a denominator of 200 greater than 0.39 and less than a two-fifths fraction. Write its numerator x.
Write a fraction with a denominator of 200 greater than 0.39 and less than a two-fifths fraction. Write its numerator x. - Division by zero
 Fraction 5 by 2. if three is added to the numerator and two is subtracted from the denominator, then the new fraction is:
Fraction 5 by 2. if three is added to the numerator and two is subtracted from the denominator, then the new fraction is: - Over fraction
 Solve an equation: p over 5 equals fraction numerator 7 p over denominator six end fraction plus 5.
Solve an equation: p over 5 equals fraction numerator 7 p over denominator six end fraction plus 5. - Adjust numerators
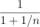 If the numerator of a fraction is increased by 2 and the denominator by 1, it becomes 5/8. If the numerator and the denominator of the same fraction are each increased by 1, the fraction becomes 1/2. Find the fraction.
If the numerator of a fraction is increased by 2 and the denominator by 1, it becomes 5/8. If the numerator and the denominator of the same fraction are each increased by 1, the fraction becomes 1/2. Find the fraction. - The numerator
 The numerator of the fraction is 5 more than its denominator. If 4 is added to the numerator and denominator, the fraction obtained is 6/5. What is that fraction?
The numerator of the fraction is 5 more than its denominator. If 4 is added to the numerator and denominator, the fraction obtained is 6/5. What is that fraction? - Numerators and denominators
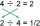 A fraction becomes 9/11, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 5/6 . Find the fraction.
A fraction becomes 9/11, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 5/6 . Find the fraction.
