Physical quantity - math word problems - page 105 of 318
A physical quantity is a term numerically describing a property or state of a physical object. For example, a physical quantity is a length, and its corresponding physical unit is a meter (symbol m). Similarly, the quantity is weight, and the unit is the kilogram (kg). Physical quantities can be divided into a scalar (has magnitude), vector (has magnitude and direction), and tensor (has magnitude and multiple directions).Number of problems found: 6343
- Angles
 The outer angle of the triangle ABC at vertex A is 113°36'. The outer angle at vertex B is 119°54'. What size is the internal angle at vertex C?
The outer angle of the triangle ABC at vertex A is 113°36'. The outer angle at vertex B is 119°54'. What size is the internal angle at vertex C? - O'clock 66554
 What is the angle of the hour and minute hands on the clock of the old tower if it is exactly eight o'clock?
What is the angle of the hour and minute hands on the clock of the old tower if it is exactly eight o'clock? - Sprinkler 36153
 The rotary sprinkler has a spray of 18m. How much land can it irrigate from one place?
The rotary sprinkler has a spray of 18m. How much land can it irrigate from one place? - Schoolyard 21183
 Adam must take 400 steps to walk around the schoolyard. How long is one side of the schoolyard in the shape of a square?
Adam must take 400 steps to walk around the schoolyard. How long is one side of the schoolyard in the shape of a square?
- Calculate 17831
 Calculate the area of a square in dm2, which has a side length of 5.8 cm.
Calculate the area of a square in dm2, which has a side length of 5.8 cm. - A rectangle 11
 A rectangle or athletic field is 100 yards wide and 500 yards long. How many square yards are on the football field?
A rectangle or athletic field is 100 yards wide and 500 yards long. How many square yards are on the football field? - Length of the arc
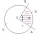 What is the arc length of a circle k (S, r=68mm), which belongs to a central angle of 78°?
What is the arc length of a circle k (S, r=68mm), which belongs to a central angle of 78°? - Plot
 The land is in the shape of a square with a dimension of 22 meters. How much will we pay for the fence around the entire plot?
The land is in the shape of a square with a dimension of 22 meters. How much will we pay for the fence around the entire plot? - Wheel
 What is the wheel diameter if the 0.57 km track turns 106 times?
What is the wheel diameter if the 0.57 km track turns 106 times?
- Calculate 81590
 Calculate the central angle if r = 72 cm and the arc length is 12.4 cm.
Calculate the central angle if r = 72 cm and the arc length is 12.4 cm. - Dimensions 70864
 Our class has dimensions of 7m in width and 13m in length. What is its area?
Our class has dimensions of 7m in width and 13m in length. What is its area? - Circumference 7335
 Calculate the length of the side of a square in cm, whose circumference is 88.8 dm
Calculate the length of the side of a square in cm, whose circumference is 88.8 dm - The formula
 The formula for the area of a circle is (Pi x r x r), where r = measure of the radius and Pi = 3.14. What is the area of a circle whose radius measures 1 cm?
The formula for the area of a circle is (Pi x r x r), where r = measure of the radius and Pi = 3.14. What is the area of a circle whose radius measures 1 cm? - Perimeter of the park
 Find the park's perimeter in meters in a diamond shape if the length of its side is 2 km.
Find the park's perimeter in meters in a diamond shape if the length of its side is 2 km.
- Sandbox
 Sandbox has an area of 32 sq ft and a length of 4 1/2 ft. What is the width of a sandbox?
Sandbox has an area of 32 sq ft and a length of 4 1/2 ft. What is the width of a sandbox? - Hectares
 The rectangular land is 350m long and 200m wide. Calculate the area in hectares.
The rectangular land is 350m long and 200m wide. Calculate the area in hectares. - Equilateral triangle v2
 An equilateral triangle has a perimeter 36 dm. What is its area?
An equilateral triangle has a perimeter 36 dm. What is its area? - 4-gon
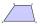 Is it true that a 4-gon whose two sides are parallel and the other two have equal length is a parallelogram?
Is it true that a 4-gon whose two sides are parallel and the other two have equal length is a parallelogram? - Flowerbed 25241
 How large should we sow an area with grass in a circular flowerbed with a radius of 4m?
How large should we sow an area with grass in a circular flowerbed with a radius of 4m?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
