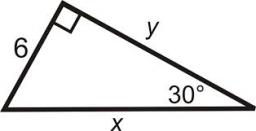
30-60-90
The longer leg of a 30°-60°-90° triangle measures 5. What is the length of the shorter leg?
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Calculate 47763
Calculate the area of an isosceles trapezoid ABCD, whose longer base measures 48 cm, the shorter base measures 3/4 of the longest base, and the leg of the trapezoid measures 2/3 of the longer base. The result is rounded to the nearest hundredth. - Rhombus
One angle of a rhombus is 136°, and the shorter diagonal is 8 cm long. Find the length of the longer diagonal and the side of the rhombus. - The ladder - RT
The ladder 16 feet reaches up 14 feet on a house wall. The 90-degree angle at the base of the house and wall. What are the other two angles or the length of the leg of the yard? - Sine theorem 2
From the sine theorem, find the ratio of the sides of a triangle whose angles are 30°, 60°, and 90°.
- Perpendicular leg
Calculate the area of a right triangle whose longer perpendicular is six dm shorter than the hypotenuse and three dm longer than the shorter perpendicular. - R triangle
Calculate the right triangle area whose longer leg is 7 dm shorter than the hypotenuse and 10 dm longer than the shorter leg. - Mr. Tolentino
Mr. Tolentino owns a piece of land that measures 86.12 meters long and 68.293 meters wide. How much longer is the length than the width?
