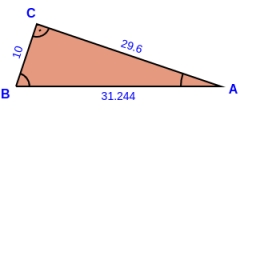
Perpendicular 41811
Calculate the area of a right triangle whose longer perpendicular is six dm shorter than the hypotenuse and three dm longer than the shorter perpendicular.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- R triangle
Calculate the right triangle area whose longer leg is 6 dm shorter than the hypotenuse and 3 dm longer than the shorter leg. - Perpendicular 5516
In a right triangle, one perpendicular is 1 m shorter than the hypotenuse. The other perpendicular is 2 m shorter than the hypotenuse. Find the lengths of all sides of the triangle. - Triangular prism
The base perpendicular triangular prism is a right triangle whose hypotenuse measures 5 cm and one cathetus 2 cm. The height of the prism is equal to 7/9 of the base's perimeter. Calculate the surface area of the prism. - Calculate 47763
Calculate the area of an isosceles trapezoid ABCD, whose longer base measures 48 cm, the shorter base measures 3/4 of the longest base, and the leg of the trapezoid measures 2/3 of the longer base. The result is rounded to the nearest hundredth.
- Prism
A right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 6 cm, has the same volume as a cube with an edge length of 1 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cube - Rectangle 79084
A rectangle whose one side measures 35m and the other is 7m shorter than the diagonal of the rectangle. Calculate the content in m². - One leg
One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle. - RT perimeter
The leg of the rectangular triangle is 7 cm shorter than the second leg and 8 cm shorter than the hypotenuse. Calculate the triangle circumference. - Calculate 78714
Calculate the size of the base and side of an isosceles triangle if the side is 1 cm longer than the base and the height to the base is 2 cm shorter than the side.
- Perpendicular 82473
In the right triangle KLM, the hypotenuse l = 9 cm and the perpendicular k = 6 cm. Calculate the size of the height vl and the line tk. - Perpendicular 32371
Calculate the area of a rectangular trapezoid whose perpendicular arm is 27 mm long and the bases are 33 mm and 19 mm long. - Perpendicular 40203 In a right triangle, one perpendicular is 5 cm longer than the other perpendicular. The diaphragm is 150 mm. Calculate the lengths of the hangings.
- Perpendiculars 36213
A right triangle with perpendiculars a = 3 cm and b = 4 cm rotates around a longer perpendicular. Calculate the volume and surface area of the resulting cone. - Right triangle eq2
The hypotenuse of a right triangle is 9 cm longer than one leg and 8 cm longer than the second leg. Determine the circumference and area of a triangle.
- Diagonal
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal. - Rhombus
Internal angles of a rhombus are in ratio 2:3. How many times is the shorter diagonal longer than the side of the rhombus? - Circumference 5254
Calculate the shorter side and the diagonal of the rectangle if one side is 2 cm longer than the other and its circumference is equal to 70 centimeters.
