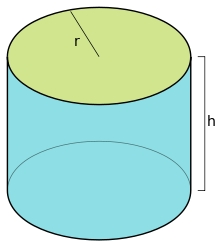
Cylinder and its circumference
The height of a cylinder is four times its circumference, c. What is the volume of the cylinder in terms of its circumference c?
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rotary cylinder 2
The base circumference of the rotary cylinder has the same length as its height. What is the surface area of the cylinder if its volume is 250 dm³? - A cylinder
A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm? - Perimeter of base
The circumference of the base of the rotating cylinder is the same as its height. What is the diameter and height of this cylinder with a volume of 1 liter? - Surface of the cylinder
Calculate the cylinder's surface area when its volume is 45 l, and the base's perimeter is three times the height.
- Circumference 66134
The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid. - Circumference 64994
Calculate the volume of the cylinder if the circumference of the base o = 31.4 cm, height v = 6.4 cm - Circumference 61654
The diamond has an area of 21.6 cm square. Its height is 4 cm. What is the circumference of the diamond?
