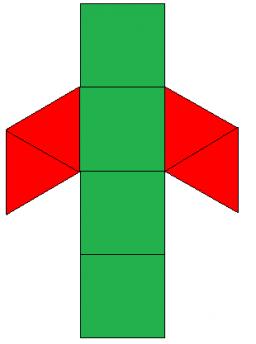
Box
The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top.
How many cm2 of cardboard do we need to cover overlap and joints that are 5% of the area of cardboard?
How many cm2 of cardboard do we need to cover overlap and joints that are 5% of the area of cardboard?
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you want to round the number?
See also our trigonometric triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Quadrilateral 82616
 Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD. - The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - A rhombus 3
 A rhombus has a side length of 6 centimeters and a height of 2 centimeters. What is the area of the rhombus in centimeters square?
A rhombus has a side length of 6 centimeters and a height of 2 centimeters. What is the area of the rhombus in centimeters square? - Height of the prism
 The volume of the quadrilateral prism is 723.6 cm³. The base of this prism is a rhombus with a side 9 cm long and a corresponding height of 6.7 cm long. Find the height of the prism.
The volume of the quadrilateral prism is 723.6 cm³. The base of this prism is a rhombus with a side 9 cm long and a corresponding height of 6.7 cm long. Find the height of the prism.
- The area
 The area of a rhombus is 143 m². If the longer diagonal is 26 m, find the shorter diagonal in inches named d1.
The area of a rhombus is 143 m². If the longer diagonal is 26 m, find the shorter diagonal in inches named d1. - Parallelogram diagonals
 Find the area of a parallelogram if the diagonals u1 = 15 cm, u2 = 12 cm, and the angle formed by them is 30 degrees.
Find the area of a parallelogram if the diagonals u1 = 15 cm, u2 = 12 cm, and the angle formed by them is 30 degrees. - Diamond and angles
 The internal angles in the diamond are 60° and 120°. Its side is 5 cm long. Find the area of a diamond.
The internal angles in the diamond are 60° and 120°. Its side is 5 cm long. Find the area of a diamond. - Irregular hexagon
 There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and193. What is its area?
There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and193. What is its area? - The diamond
 The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond.
The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond.
- Parallelogram 43601
 Calculate the area and perimeter of a parallelogram if a = 5.2cm Va = 4cm (it is a parallelogram, not a triangle)
Calculate the area and perimeter of a parallelogram if a = 5.2cm Va = 4cm (it is a parallelogram, not a triangle) - Equation of the circle
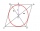 Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4].
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Four prisms
 Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t
Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t - Quadrilateral prism
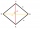 Calculate the surface of a quadrilateral prism according to the input: Area of the diamond base S1 = 2.8 m2, length of the base edge a = 14 dm, the prism height 1,500 mm.
Calculate the surface of a quadrilateral prism according to the input: Area of the diamond base S1 = 2.8 m2, length of the base edge a = 14 dm, the prism height 1,500 mm. - Circumference 21603
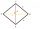 The circumference of the diamond is 29.6dm. a - calculate the length of its side b - calculate the area of the diamond if its height measures 5 dm
The circumference of the diamond is 29.6dm. a - calculate the length of its side b - calculate the area of the diamond if its height measures 5 dm
- Two patches
 Peter taped the wound with two rectangular patches (one over the other to form the letter X). The area sealed with both patches simultaneously had an area of 40cm² and a circumference of 30cm. One of the patches was 8cm wide. What was the width of the sec
Peter taped the wound with two rectangular patches (one over the other to form the letter X). The area sealed with both patches simultaneously had an area of 40cm² and a circumference of 30cm. One of the patches was 8cm wide. What was the width of the sec - Diamond - simple
 Calculate the circumference and area of the diamond if the side is 5 cm long and the height is 3 cm long.
Calculate the circumference and area of the diamond if the side is 5 cm long and the height is 3 cm long. - Diamond diagonals
 Find the diamond diagonal's lengths if the area is 156 cm² and the side is 13 cm long.
Find the diamond diagonal's lengths if the area is 156 cm² and the side is 13 cm long.
