Four prisms

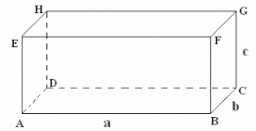
Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume?
a) 3000 cm²
b) 300 cm²
c) 3000 cm³
d) 300 cm³

Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of the prism is 5dm. What is the volume of the prism?
a) 20 250
b) 450
c) 40,500
d) 4,050

Question No.3: A regular square prism with a square base has a volume of 63 cm³ and a height of 7 cm. Calculate its surface.
a) 756
b) 102
c) 63
d) 414

Question No.4: Calculate the surface of a square prism high vh = 2 dm, the base of which is a trapezoid with bases z1 = 10cm, z2 = 8cm, height v = 4cm and with arms long r1 = r2 = 5cm.
a) 128 cm²
b) 596 cm²
c) 632 cm²
d) 532 cm²

Correct answer:

V₁ =  300 cm³
V₂ =  30000 cm³
S₃ =  102 cm²
S₄ =  632 cm²

Step-by-step explanation:

$$\begin{gathered} a_1=2.5\text{ cm } \\ {b}_1=100\text{ mm}\to \text{ cm}=100\mathrm{/}10\text{ cm}=10\text{ cm } \\ {c}_1=12\text{ cm } \\ {V}_1=a_1\cdot b_1\cdot c_1=2.5\cdot 10\cdot 12=300{\text{cm}}^3 \end{gathered}$$

$$\begin{gathered} a_2=30\text{ cm } \\ {b}_2=20\text{ cm } \\ {c}_2=5\text{ dm}\to \text{ cm}=5\cdot 10\text{ cm}=50\text{ cm } \\ {V}_2=a_2\cdot b_2\cdot c_2=30\cdot 20\cdot 50=30000{\text{cm}}^3 \end{gathered}$$

$$\begin{gathered} V_3=63{\text{cm}}^3 \\ c=7\text{ cm } \\ {S}_1=V_3\mathrm{/}c=63\mathrm{/}7=9{\text{cm}}^2 \\ a=\sqrt{S_1}=\sqrt{9}=3\text{ cm } \\ {S}_3=4\cdot a\cdot c+2\cdot S_1=4\cdot 3\cdot 7+2\cdot 9=102{\text{cm}}^2 \end{gathered}$$

$$\begin{gathered} v_4=2\text{ dm}\to \text{ cm}=2\cdot 10\text{ cm}=20\text{ cm } \\ {z}_1=10\text{ cm } \\ {z}_2=8\text{ cm } \\ v=4\text{ cm } \\ {r}_1=5\text{ cm } \\ {r}_2=5\text{ cm } \\ {S}_{44}={\displaystyle \frac{z_1+z_2}{2}}\cdot v={\displaystyle \frac{10+8}{2}}\cdot 4=36{\text{cm}}^2 \\ {S}_4=(z_1+z_2+r_1+r_2)\cdot v_4+2\cdot S_{44}=(10+8+5+5)\cdot 20+2\cdot 36=632{\text{cm}}^2 \end{gathered}$$

Try another example

Related math problems and questions:

• Remainders
  It is given a set of numbers { 170; 244; 299; 333; 351; 391; 423; 644 }. Divide this numbers by number 66 and determine set of remainders. As result write sum of this remainders.
• Tablecloths
  The restaurant has sixty-two square tablecloths with a side length of 150 cm and 36 rectangular tablecloths with dimensions of 140 cm and 160 cm. A) How many meters of hemming ribbon will be needed if we add 50 cm to each tablecloth? B) The ribbon sale in
• Cuboid - volume and areas
  The cuboid has a volume of 250 cm³, a surface of 250 cm² and one side 5 cm long. How do I calculate the remaining sides?
• Tank full
  2 hl of water were poured into a block-shaped tank with dimensions of 450 mm and 600 mm and a height of 900 mm. How many liters of water need to be added to keep the tank full?
• Annual income
  The annual income (in thousands of $) of fifteen families is 60, 80, 90, 96, 120, 150, 200, 360, 480, 520, 1060, 1200, 1450, 2500, 7200. Calculate the harmonic and geometric mean.
• Concert
  On a Concert were sold 150 tickets for CZK 360, 235 tickets for 240 CZK and 412 for 180 CZK. How much was the total revenues for tickets?
• Cuboid walls
  Calculate the cuboid volume if its different walls have an area of 195cm², 135cm², and 117cm².
• Pool tiles
  The pool is 25m long, 10m wide, and 160cm deep. How many m² of tiles will be needed on the walls and the pool? How many tiles are needed when 1 tile has a square shape with a 20cm side? How much does it cost when 1m² of tiles costs 258 Kc?
• Edge of prism
  The regular quadrilateral prism has a surface of 250 dm², its shell has a content of 200 dm². Calculate its leading edge.
• Seeds
  The field has a rectangular shape with dimensions of 128 m and 350 m. How many kg of seed are needed for sowing if the 1 m² will consume 25 g of seeds?
• Height of the cylinder
  The cylinder volume is 150 dm cubic, the base diameter is 100 cm. What is the height of the cylinder?
• Gasoline price 2
  During the COVID-19 pandemic new gasoline price shceme is given by Marilou's Gas Station to help our drivers. On their purchase, the first 4 liters cost Php120.00, while the succeeding 1 1/2 liters would cost Php10.00 more than the cost of a liter. If joh
• Painter 3
  Dad want to paint wall high 250 cm wide and 230 cm with wallpaper. How many meters must buy wallpaper if wallpaper width is 60 cm?
• The Scout Tent
  The Scout Tent has a rectangular wooden underlay with dimensions of 220 cm and 150 cm. How much canvas is needed for a 170 cm high of pyramid roof?
• The tractor
  The tractor sows an average of 1.5 ha per hour. In how many hours does it sows a rectangular trapezoid field with the bases of 635m and 554m and a longer arm 207m?
• Sails
  We known heights 220, 165, and 132 of sail. It has a triangular shape. What is the surface of the sail?
• Prism
  The base of the prism is a rhombus with a side 30 cm and a height 27 cm long. The height of the prism is 180% longer than the side length of the rhombus. Calculate the volume of the prism.