Sugar - cuboid
Pablo received from his master a cuboid composed of identical sugar cubes with a count between 1000 and 2000. The Pejko eat sugar cubes in layers.
On the first day, eat one layer from the front. On the second day, one layer from the right, and on the third day, one layer above. However, those three layers were each the same number of cubes. Find out how many cubes had the original cuboid. Find all possibilities.
On the first day, eat one layer from the front. On the second day, one layer from the right, and on the third day, one layer above. However, those three layers were each the same number of cubes. Find out how many cubes had the original cuboid. Find all possibilities.
Correct answer:

Tips for related online calculators
Do you solve Diofant problems and looking for a calculator of Diofant integer equations?
Tip: Our volume units converter will help you convert volume units.
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- The difference 6
 The difference between a number and 15 is multiplied by -3, and the result is - 30
The difference between a number and 15 is multiplied by -3, and the result is - 30 - Determine 216
 Determine the quotient; (-20) divided by ( -4) =? A) +6 B) - 6 C) +5 D) -5
Determine the quotient; (-20) divided by ( -4) =? A) +6 B) - 6 C) +5 D) -5 - Temperature minus
 On a very cold day in January, the temperature started at -12 degrees. The temperature rose 20 degrees during the day. That evening, the temperature fell 10 degrees. What is the temperature at the end of the day?
On a very cold day in January, the temperature started at -12 degrees. The temperature rose 20 degrees during the day. That evening, the temperature fell 10 degrees. What is the temperature at the end of the day? - Add, sub and div
 Find the value of (52 - 14 - 8 - 7)/(15 - 4 * 2) Give your answer as a mixed number in its simplest form.
Find the value of (52 - 14 - 8 - 7)/(15 - 4 * 2) Give your answer as a mixed number in its simplest form.
- Positive products
 Which of these products is positive? Select all that apply. a) -0.2 * (12.5) b) -4.7 * (-1)
Which of these products is positive? Select all that apply. a) -0.2 * (12.5) b) -4.7 * (-1) - Arithmetic sequence
 Determine the sum of the first 12 terms of an AP (arithmetic sequence) if a4 is equal to 7 and a8 is equal to minus 1.
Determine the sum of the first 12 terms of an AP (arithmetic sequence) if a4 is equal to 7 and a8 is equal to minus 1. - Negative number 2
 Haley is trying out a new racing game on her tablet. Her score decreases by 100 points when her driving car gets a flat tire. What integer represents the change in Haley's score when she gets a flat tire?
Haley is trying out a new racing game on her tablet. Her score decreases by 100 points when her driving car gets a flat tire. What integer represents the change in Haley's score when she gets a flat tire? - Minus round
 The outdoor temperature yesterday reached a low of −4.5°F. Between what two integers was the temperature?
The outdoor temperature yesterday reached a low of −4.5°F. Between what two integers was the temperature? - Cody states
 Cody states that 1/4 + ( - 6/8 ) = 1 whole, while Eddie says that it is - 1/2. Who is correct? Justify your answer and explain your thinking.
Cody states that 1/4 + ( - 6/8 ) = 1 whole, while Eddie says that it is - 1/2. Who is correct? Justify your answer and explain your thinking.
- Write 9
 Write the numbers given in the place value table in decimal form. Hundreds Tens. Ones. Tenths. 6. 1. 5. 4 8. 3. 2. 5 7. 9. 0. 3 1. 0. 3. 1 4. 8. 0. 7
Write the numbers given in the place value table in decimal form. Hundreds Tens. Ones. Tenths. 6. 1. 5. 4 8. 3. 2. 5 7. 9. 0. 3 1. 0. 3. 1 4. 8. 0. 7 - The high 2
 The high for Wednesday was −10°, and the low was −23°. How many degrees did the temperature drop on Wednesday?
The high for Wednesday was −10°, and the low was −23°. How many degrees did the temperature drop on Wednesday? - Negative numbers
 Ahmed's teacher asks him to l: "start with +2, then multiply by -1, then subtract 3, then divide by -1, then add -6". What should Ahmed's answer be?
Ahmed's teacher asks him to l: "start with +2, then multiply by -1, then subtract 3, then divide by -1, then add -6". What should Ahmed's answer be? - At 7:00
 At 7:00 AM, Peter took a reading of the outside temperature of 40℉. During the day, the temperature dropped 9℉, rose 5℉, and then dropped again another 2℉. What was the outside temperature at after his last reading?
At 7:00 AM, Peter took a reading of the outside temperature of 40℉. During the day, the temperature dropped 9℉, rose 5℉, and then dropped again another 2℉. What was the outside temperature at after his last reading? - Two hours
 Two hours ago, the temperature was 8°F. The temperature is now -4°F. What was the change in temperature for the past two hours?
Two hours ago, the temperature was 8°F. The temperature is now -4°F. What was the change in temperature for the past two hours?
- LCM or HCF
 Find the lowest common multiple of these two numbers: 105 226
Find the lowest common multiple of these two numbers: 105 226 - Temperature dropping
 If the temperature drops 2 degrees for 6 hours and the starting temperature is 10 degrees, what will the new temperature be?
If the temperature drops 2 degrees for 6 hours and the starting temperature is 10 degrees, what will the new temperature be? - Identify 4
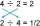 Identify the whole number whose reciprocal has a decimal equivalent between 0.2 and 0.3. Explain.
Identify the whole number whose reciprocal has a decimal equivalent between 0.2 and 0.3. Explain.
