Ball bearings
One bearing is selected from the shipment of ball bearings. It is known from previous deliveries that the inner bearing radius can be considered a normal N distribution (µ = 0.400, σ2 = 25.10^−6). Calculate the probability that the selected radius will exceed 0.405 for the selected bearing.
Your answer:
Your answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
Looking for a standard deviation calculator?
Would you like to compute the count of combinations?
Looking for a statistical calculator?
Looking for a standard deviation calculator?
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
statisticscombinatoricsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Lifespan
The lifetime of a light bulb is a random variable with a normal distribution of x = 300 hours, σ = 35 hours. a) What is the probability that a randomly selected light bulb will have a lifespan of more than 320 hours? b) To what value of L hours can the la - Probability
A restaurant always counts the cash register at the end of the day so that the employees can divide their tips. It has been found that the daily tips follow a normal distribution with a mean of €130 and a standard deviation of €60. What is the probability - Probability
In a batch of 500 products, there are 10 defective items. In a statistical inspection, 40 products are selected at random from the batch without replacement. The batch is considered satisfactory if there is at most one defective product among the 40 inspe - Rice - packaging line
An automatic machine weighs rice into packages on a packaging line. Suppose that the mass of rice in a package is a random variable which has a normal probability distribution with mean value (Greek letter Mu) = 500 g and standard deviation (Greek letter - Probability - products
Based on previous inspection, it is known that 3% of defective products occur during the manufacturing of a certain product. a) Calculate the probability that among 100 randomly selected products there are exactly 2 defective ones, assuming each product i - Statistics quiz
Fill in the missing word. 1. in a data set, the mean, median, and mode are measured of ________________ 2. "The manipulation of variables under controlled conditions" is the data collection method known as______________ 3. in a normal distribution, the ar - Z-score test
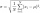The fish weights in a certain lake are normally distributed with a mean of 11 lb and a standard deviation of 6. If four fish are randomly selected, what is the probability that the mean weight will be between 8.6 and 14.6 lb? Your answer should be a decim
