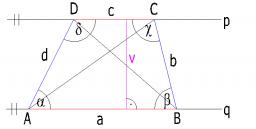
Trapezoid - diagonal
A trapezoid has a length of diagonal AC crossed with diagonal BD in the ratio of 2:1. The triangle created by points A, the cross point of diagonals S, and point D has an area 164 cm2. What is the area of the trapezoid?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Trapezium diagonals
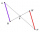It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - The diagonals 2
The diagonals AC and BD of a rectangle ABCD intersect at a point O. If OA=4cm, find AC and BD. - Diagonal intersect
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - Quadrilateral 27693
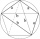Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125°
- Diagonals of rhombus
Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm. - Rectangular trapezoid
Calculate the area of a rectangular trapezoid with a right angle at point A and if |AC| = 4 cm, |BC| = 3 cm, and the diagonal AC is perpendicular to the side BC. - Rectangular trapezoid
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters
