Isosceles trapezoid
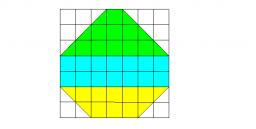
Calculate the area of an isosceles trapezoid whose bases are in the ratio of 4:3; leg b = 13 cm and height = 12 cm.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
Do you want to convert length units?
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Do you want to convert length units?
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Isosceles trapezoid
The bases of the isosceles trapezoid are in the ratio of 5:3. The arms have a length of 5 cm and height = 4.8 cm. Calculate the circumference and area of a trapezoid. - Isosceles trapezoid
Calculate the area of an isosceles trapezoid whose bases are at a ratio of 5:3. The arm is 6cm long and 4cm high. - Cross-section 23491
The cross-section of the railway embankment is an isosceles trapezoid, the bases of which are in a ratio of 5:3. The arms have a 5 m embankment height v = 4.8 m. Calculate the section area S. - Triangular prism
Calculate the volume and surface of the triangular prism ABCDEF with the base of an isosceles triangle. Base's height is 16 cm, leg 10 cm, base height vc = 6 cm. The prism height is 9 cm.
- Calculate 47763
Calculate the area of an isosceles trapezoid ABCD, whose longer base measures 48 cm, the shorter base measures 3/4 of the longest base, and the leg of the trapezoid measures 2/3 of the longer base. The result is rounded to the nearest hundredth. - IS trapezoid
Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Quadrilateral prism
Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated?
